Gauss's Law

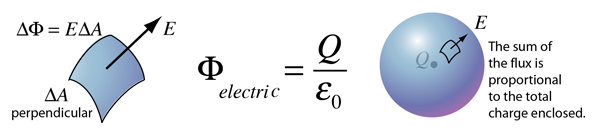
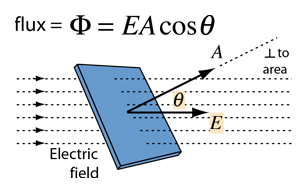
The electric flux through an area is defined as the electric field multiplied by the area of the surface projected in a plane perpendicular to the field. Gauss's Law is a general law applying to any closed surface. It is an important tool since it permits the assessment of the amount of enclosed charge by mapping the field on a surface outside the charge distribution. For geometries of sufficient symmetry, it simplifies the calculation of the electric field.

Another way of visualizing this is to consider a probe of area A which can measure the electric field perpendicular to that area. If it picks any closed surface and steps over that surface, measuring the perpendicular field times its area, it will obtain a measure of the net electric charge within the surface, no matter how that internal charge is configured.

Gauss' Law, Integral Form

The area integral of the electric field over any closed surface is equal to the net charge enclosed in the surface divided by the permittivity of space. Gauss' law is a form of one of Maxwell's equations, the four fundamental equations for electricity and magnetism.

Electric Flux

The concept of electric flux is useful in association with Gauss' law. The electric flux through a planar area is defined as the electric field times the component of the area perpendicular to the field. If the area is not planar, then the evaluation of the flux generally requires an area integral since the angle will be continually changing.

When the area A is used in a vector operation like this, it is understood that the magnitude of the vector is equal to the area and the direction of the vector is perpendicular to the area.

Applications of Gauss' Law

Gauss' law is a powerful tool for the calculation of electric fields when they originate from charge distributions of sufficient symmetry to apply it.