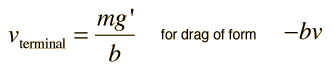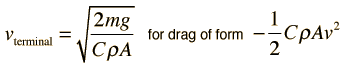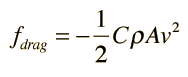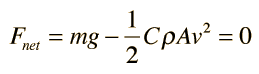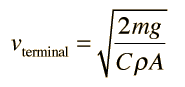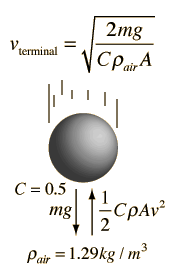Quadratic Velocity Dependence
For large objects moving through air, the air resistance is approximately proportional to the square of the velocity. The form of the resistance is
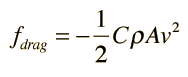
where ρ is the air density, A the crosssectional area, and C is a numerical drag coefficient. The drag coefficient C is 0.5 for a spherical object and can reach 2 for irregularly shaped objects according to Serway. An object falling through the air will reach a terminal velocity when the drag force is equal to the weight:
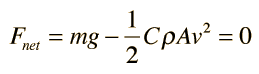
This gives a terminal velocity
|
Index
Fluid friction
Reference
Serwary & Beichner
Ch 6 |