Wave-Particle Duality: Light
Does light consist of particles or waves? When one focuses upon the different types of phenomena observed with light, a strong case can be
built for a wave picture:
By the turn of the 20th century, most physicists were convinced by phenomena like the above that light could be fully described by a wave, with no necessity for invoking a particle nature. But the story was not over.
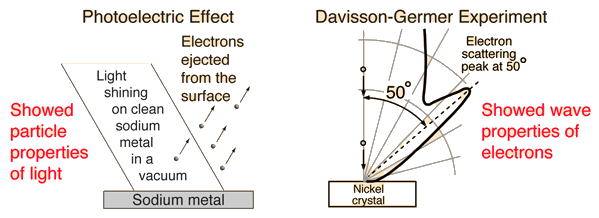
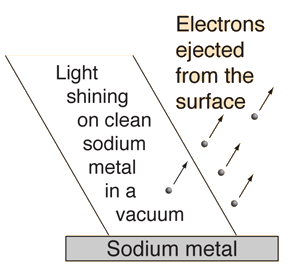
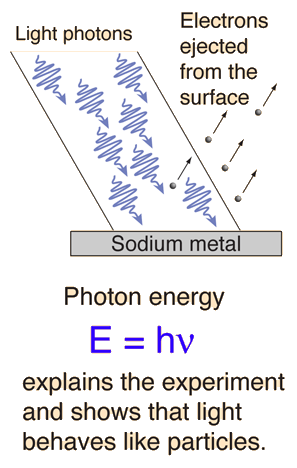
Most commonly observed phenomena with light can be explained by waves. But the photoelectric effect suggested a particle nature for light. Then electrons too were found to exhibit dual natures.
 | There is a considerable amount of discussion in the literature about whether reflection and refraction of light at an interface where the medium changes can be described in particle terms. For practical applications of geometrical optics, treating light as a wave phenomenon is adequate. |
Newton's corpuscular theory: Newton proposed that light was composed of corpuscles that traveled in straight lines. That worked fine for reflection, because the bouncing of either particles or waves off a planar surface follows the same law of reflection. But to explain refraction, he had to presume that the particles traveled faster in a more optically dense material. But Foucault's 1850 experiment showed that light traveled more slowly in such media, so that version of a particle theory of light had to be set aside.
Huygens wave theory: Presuming that light was composed of waves, in 1678 Huygens proposed that each point of a light wavefront could be considered to be the source of a spherical wave. The Huygens' principle helped develop the wave theory of light and it was further developed by Fresnel and Kirchhoff.
Quantum view of light: The photoelectric effect introduced evidence that light exhibited particle properties on the quantum scale of atoms. At least light can achieve a sufficient localization of energy to eject an electron from a metal surface. So it might be implied that there must be a particle treatment of refraction of light, but for ordinary optics the wave view of light is the practical approach.
|