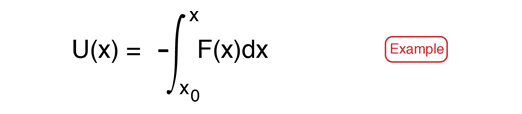Potential Energy
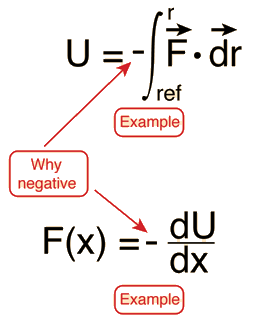
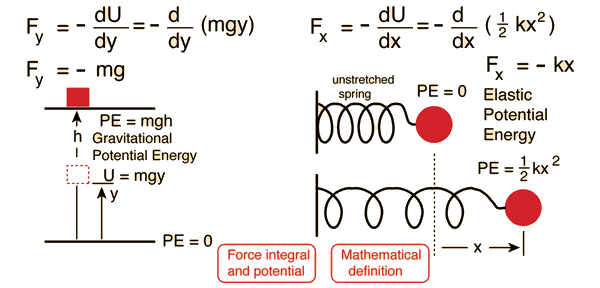
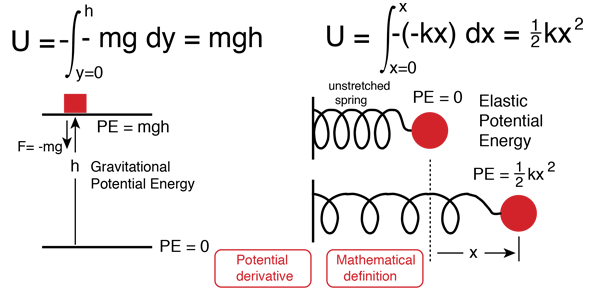
Potential energy is energy which results from position or configuration. The SI unit for energy is the joule = newton x meter in accordance with the basic definition of energy as the capacity for doing work. An object may have the capacity for doing work as a result of its position in a gravitational field (gravitational potential energy), an electric field (electric potential energy), or a magnetic field (magnetic potential energy). It may have elastic potential energy as a result of a stretched spring or other elastic deformation.
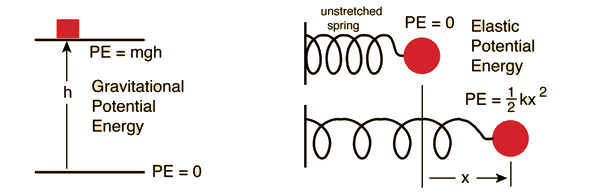
Mathematical definition
Energy concepts
| HyperPhysics***** Mechanics | R Nave |