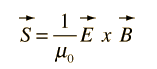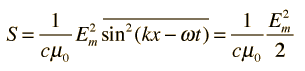Electromagnetic Wave Equation
The wave equation for a plane electric wave traveling in the x direction in space is

with the same form applying to the magnetic field wave in a plane perpendicular the electric field. Both the electric field and the magnetic field are perpendicular to the direction of travel x. The symbol c represents the speed of light or other electromagnetic waves. The wave equation for electromagnetic waves arises from Maxwell's equations. The form of a plane wave solution for the electric field is
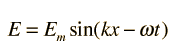
and that for the magnetic field
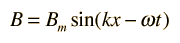
To be consistent with Maxwell's equations, these solutions must be related by
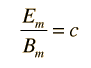
The magnetic field B is perpendicular to the electric field E in the orientation where the vector product E x B is in the direction of the propagation of the wave.
| Transport of energy by electromagnetic waves |
Wave concepts
Electromagnetic wave concepts
Electromagnetic spectrum
| HyperPhysics*****Electricity and Magnetism | R Nave |