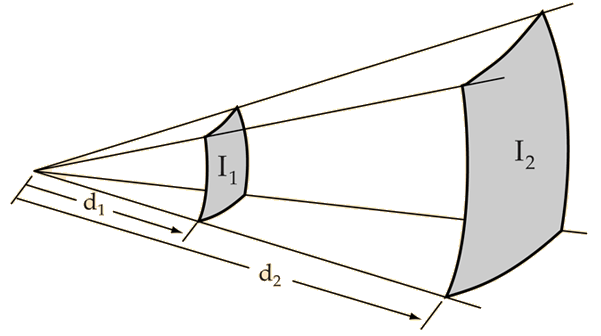
The Inverse Square Law Problem

In an open area, sound drops off according to the inverse square law. In an auditorium where the front seats are 6 meters (20 ft) from the sound source and the back seats are 60 m (200 ft) from the sound source, the sound intensity would drop by a factor of 100 ( = 20 decibels ) between the front seats and the back seats if it followed this pattern. This is an unacceptable loss which is prevented partially by reverberation.

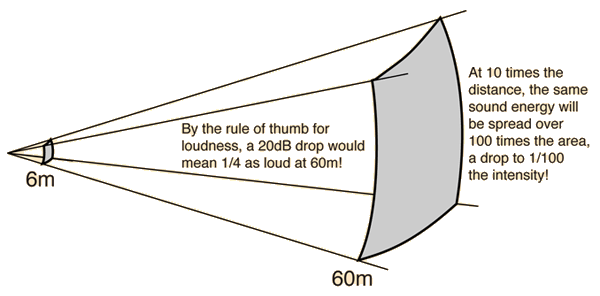
For a sound in the midrange of human hearing, one can anticipate that a drop of 20db would be experienced as about one-fourth as loud by the rule of thumb for loudness. But for sounds in the low range of human hearing, like the bottom end of the piano's range, the loss in effective loudness is even more severe because of the progressive loss of low frequencies for the human ear. This produces another problem for auditorium acoustics called the bass-loss problem.

Inverse Square Law Example

If a sound level of 90 decibels is produced at the front row of an auditorium and the back row is 10 times as far away, then the sound intensity will fall by a factor of 100 if the inverse square law applies. A factor of 100 is a drop of 20 decibels to a level of 70 decibels on the back row. 90 dB is a loud sound which would be assigned a dynamic level ff , but 70 dB is a medium soft sound, dynamic level mp.

Inverse Square Law by Ratio

Expressed as a ratio, the inverse square law takes the form

If d2 = x d1 then I2 = I1/( ) = I1

If I1 = dB, then I2 = dB

You can explore numerically to confirm that doubling the distance drops the intensity by about 6 dB and that 10 times the distance drops the intensity by 20 dB.