Division of Energy Between Photons and Massive Particles
One of the ideas associated with modeling the Big Bang is that the further back in time you project, the more the universe is dominated by photons. We think of today's universe as mostly matter, but the energy of the early universe was mostly photon energy with massive particles playing a very small role.
The amount of energy in radiation in today's universe can be estimated with the use of the Stefan- Boltzmann law, considering that the universe is filled with blackbody radiation at a temperature of 2.7 K. The energy density in this equilibrium radiation is given by
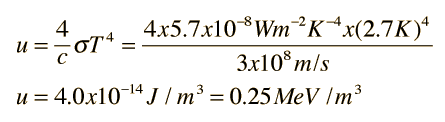
There is also a background energy in neutrinos which is expected to have a temperature of about 1.9 K, and there are 7/4 as many of them as photons according to the standard model. Treating them as massless particles would give an energy density of about 0.11 MeV/m3, so the total energy density in photons and neutrinos is about
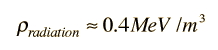 |
|
One current estimate of the amount of mass in the current universe is
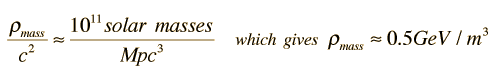 ,
,Note that this energy in massive particles is that of ordinary baryonic matter, but the associated density falls far short of the critical density that apparently characterizes the universe. The density is typically expressed in terms of a density parameter, Ω.
| Relate to temperature and expansion time |
Reference
Rohlf
Ch. 19
| HyperPhysics***** Astrophysics | R Nave |
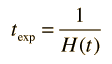 ,
,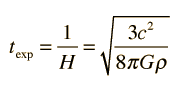 .
. .
.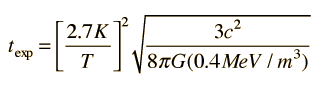 .
.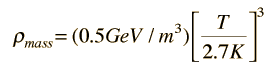 .
.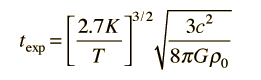 .
.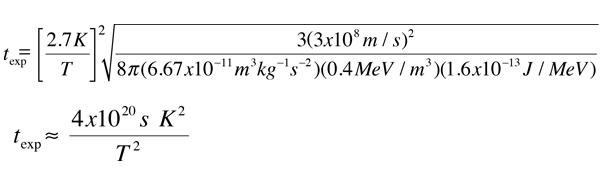 .
.