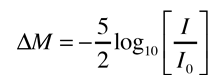Stellar Parallax
A nearby star's apparent movement against the background of more distant stars as the Earth revolves around the Sun is referred to as stellar parallax.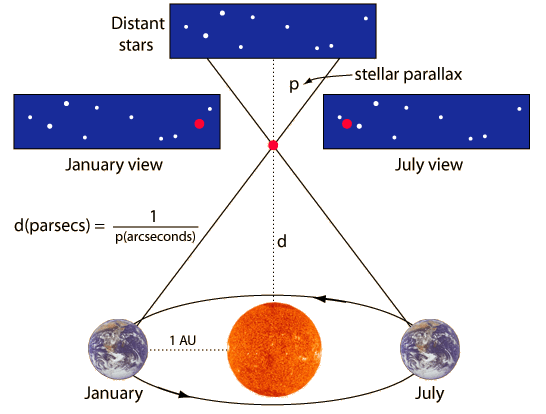
This exaggerated view shows how we can see the movement of nearby stars relative to the background of much more distant stars and use that movement to calculate the distance to the nearby star.
The parallax can be used to measure the
distance to the few stars which are
close enough to the Sun to show a
measurable parallax. The distance to
the star is inversely proportional to
the parallax. The distance to the star in
parsecs is given by The nearest star is proxima centauri, which exhibits a parallax of 0.762 arcsec, and therefore is 1.31 parsecs away. |

|
The distance at which parallax can be reliably measured has now been greatly extended by space-based instruments like the Hipparcos satellite.
Distance measurement
References
Kaufman, Universe
Chaisson & McMillan
| HyperPhysics***** Astrophysics | R Nave |