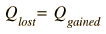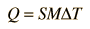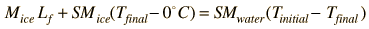SPECIFIC HEAT AND HEAT OF FUSION
Part I. Specific heat
HEAT EXCHANGE: When two or more objects at different temperatures are brought together in an isolated environment, they eventually reach the same temperature by the process of heat exchange. That is, warmer materials transfer heat to colder materials until their temperatures are the same. The energy which is being transferred is referred to as internal energy, energy associated with random molecular motion on the microscopic scale. This energy can be divided into kinetic energy and the potential energy arising from the intermolecular attractive forces in the material. If we have two isolated substances and assume no loss to the environment, then the conservation of energy principle implies that the energy lost by one substance must be gained by the other. Letting Q stand for the quantity of heat, this idea may be expressed as
| (1) |
Temperature is a measure of the average kinetic energy of the random molecular motion. As a body gains or loses kinetic energy its temperature will increase or decrease. The temperature change is symbolized by DT where
| (2) |
Although the internal energy possessed by an object is directly proportional to its mass, it does not follow that two objects of the same mass and temperature have the same amount of internal energy. Temperature reflects only the kinetic energy portion of the internal energy, so a substance with a greater fraction of its internal energy in the form of potential energy will have a greater internal energy at a given temperature. Thus a gram of water at 50°C will have a much larger internal energy than a gram of copper at 50°C and it will take a much larger energy input to heat the water to 60°C than to produce the same temperature change in copper. This property is reflected in the quantity called the specific heat (S). The specific heat is defined as the quantity of heat required to raise the temperature of 1 gram of a substance 1°C.
Taking all of the above into consideration, the quantity of heat lost or gained by a body can be calculated by the relation
| (3) |
where M is the mass of the substance.
* Internal energy can be measured in calories. The dietary Calorie is a kilocalorie or 1000 calories.
LABORATORY EXERCISE: The specific heat of a metal sample will be determined. A summary of the experiment follows, and the equipment diagram below will show you the names of the pieces of equipment used.
Heated metal is poured into an insulated container of cool water. Since care will be taken to prevent heat from entering or escaping the container, it is assumed that the amount of energy lost by the hot metal is gained by the water.
From relationships (2) and (3) the amount of heat gained by the water can be computed. Since this must be the amount of heat lost by the metal, relationship (3) can be applied to the metal sample. When substitution of the known quantities is done, the remaining unknown quantity is the specific heat of the metal, which is then calculated from the equation. Once the metal is identified, the % deviation from the standard specific heat can be computed.
PROCEDURE:
1. Fill the boiler about 2/3 full of water. Begin heating immediately.
2. Place a known mass of metal in the boiler cup as follows:
a. Determine the mass of the empty boiler cup.
b. Fill the boiler cup about 2/3 full of the metal material provided and redetermine the mass.
3. Carefully place the boiler cup into the boiler so the metal can begin heating.
4. Using the graduated cylinder, pour 100 ml or a convenient volume of cool water which will fill the calorimeter cup about 2/3 full. Since water has a density of 1 gram/cm3 = 1 gram/ml, the number of grams equals the number of ml of water.
5. Place the 110°C thermometer in the boiler cup and carefully work it down into the metal particles.
6. When the metal is nearly finished heating, place the 50°C thermometer into the calorimeter and record the initial temperature of the water.
7. When the metal reaches about 95°C (which is to be the initial temperature of the metal), quickly remove the boiler cup from the boiler and pour the hot metal into the calorimeter. Record the initial temperature of the metal.
8. Quickly put the lid on the calorimeter. place the 50°C thermometer through the hole in the top to the lid and stir the metal and water GENTLY.
9. After the mercury in the thermometer readjusts its level and ceases moving, record the temperature. This is the final temperature of the metal and the water. Record the temperature.
10. Calculate the specific heat of the metal from the data you have collected. Make a tentative identification the the metal by referring to the table to specific heats provided. After confirming your identification with your lab instructor, calculate the percent deviation of your result from the standard value as follows:
| (4) |
Part II. Heat of Fusion of Water
CHANGE OF PHASE-SOLID TO LIQUID: An increase in internal energy is required to convert a solid to a liquid. Conversely, a reduction in internal energy can cause liquids to freeze or solidify. These solid-liquid phase changes occur without a change in temperature, i.e., no change in average kinetic energy occurs. The heat of fusion of a substance is the heat exchange required to melt one gram of the substance (calories/gm).
In this part of the experiment, the heat of fusion of water will be determined. Warm water will be used to melt ice, and the change in temperature of the water in the calorimeter will be used to compute the amount of energy extracted from the water to melt the ice. The ice must absorb heat in order to melt. The heat absorbed can be expressed as
Heat gained by ice = Heat lost by water
| (5) |
where Lf is the symbol for the heat of fusion in calories/gram. The necessary heat will be transferred from the warm water to the ice.
PROCEDURE:
1. Warm some water to about 15°C above room temperature. (Water from the hot water tap may be hot enough.)
2. Mass the empty calorimeter with the styrofoam cup and record its mass. Remass it when it is approximately half full of the warm water and record the new mass. This must be done carefully, as it cannot be repeated later. Calculate the mass of the warm water.
3. Gently stir the water and record its temperature using the 50°C thermometer.
4. Dry pieces of the ice provided with a piece of paper towel. Slip them into the water, stirring gently and being careful not to splash water out. Continue to stir the water while adding ice to it one piece at a time. When the temperature of the water is approximately 15°C below room temperature, stop adding ice. When the last bit of ice has melted, record the lowest temperature that the water reaches. This temperature is the final temperature of the warm water and of the ice water.
5. Mass the calorimeter and its contents and determine the mass of ice that was added.
6. Calculate the heat of fusion and find the percent deviation from the accepted value 79.72 cal/gm.
QUESTIONS:
1. How many calories are required to heat 10 grams of water by 20°C?
2. What temperature change would the above amount of energy cause in 10 grams of lead?
3. How would the results for the heat of fusion of water have been affected if the ice were not dried before being placed in the calorimeter? Would this have made the measured heat of fusion larger or smaller?
Specific heats (cal/gm °C)
| Lead | .031 |
| Copper | .092 |
| Aluminum | .217 |
| Iron | .11 |
| Silver | .056 |
Apparatus movie