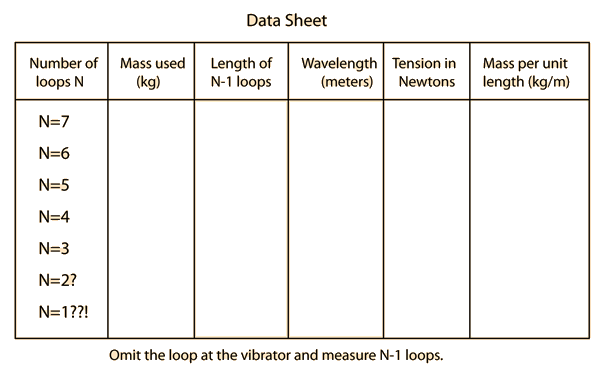
Standing Waves on a String
Standing waves are produced on a string when equal waves travel in opposite directions. When the proper conditions are met, the interference between the traveling waves causes the string to move up and down in segments, as illustrated below. This segment vibration gives no appearance of motion along the length of the string. The phenomenon is called a standing wave or stationary wave and corresponds to a resonant vibration of the string.

If a light, flexible string is attached to a vibrator and the other end passed overr a fixed pulley to a weight hanger, the necessary conditions for standing waves can be met. Waves from the vibrator travel down the string and are reflected at the pulley. When the tension and length of the string are properly adjusted, these two oppositely directed wave trains superimpose to give alternate regions of no vibration, N (see figure) and regions of maximum vibration, A. These regions N and A are called nodes and antinodes, respectively, and the segment between two nodes is called a loop. The velocity, v, of a wave on a stretched string is given by:
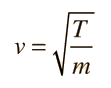 | (1) |
where T is the stretching force (tension) and m is the mass per unit length of the string. If the general wave equation:
 | (2) |
is combined with the above equation, the frequency of the vibrator is given by the relation:
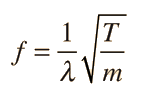 | (3) |
where λ is the wavelength of the wave. Examination of the figure, in which the full line represents the original wave train and the dashed line the reflected wave train, will show that the distance between two nodes is one half wavelength. In this experiment, you will be given the frequency f = 60Hz and can then determine the quantity T/f2λ2. The mass per unit length m of the string is to be calculated from:
 | (4) |
Procedure
1. Attach the string to the vibrator and add weights to the weight holder until a distinct standing wave with about six loops is produced (or as many loops as possible). If the weights available are not small enough for the fine adjustment, a small movement of the pulley toward or away from the vibrator may accomplish the desired result. For best accuracy, make small adjustments in the tension to get the maximum amplitude of vibration.
2. Omitting the loop nearest the vibrator, measure and record the total length of the remaining loops. Record the number of loops and the stretching force
3. Keep the distance between the pulley and the vibrator the same, except for small adjustments, and increase the stretching force until a distinct standing wave is produced with one less loop. Again measure the loops and record the data as in step 2.
4. Continue the process of reducing the number of loops by one until you have added enough to produce only two loops. Record all data as before.
5. Compute the wavelength for each of the trials.
6. Convert the stretching force to newtons by multiplying the mass in kilograms by the acceleration of gravity, g = 9.8 m/sec2.
7. Calculate the values of mass per unit length m = T/f2λ2 for each of the different loop patterns.
Equipment: String Resonance
- Vibrator and string
- Set of masses and mass hanger to attach to string.
- Meter stick
- Two vertical rods, 90° clamp.
- Small pulley on rod.