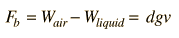Density and Buoyancy
This exercise is about density (mass per unit volume) and how to determine it. The provided materials are a metal cylinder and two mineral samples.
|
What do you think? Which can be determined more accurately, mass or volume? Why?
If you determined volume by (1) direct measurement, (2) seeing how much water it displaces, and (3) using Archimedes' principle, which would you expect to be most accurate and why?
Examine the light and dark rocks. Which is heavier?
Which rock would you judge to be the most dense?
|
Introduction
Mass is a physical property which all objects possess, but objects of the same size can have different masses and weights. This difference is characterized by another property, density. Density is defined as the ratio of an object's mass to its volume:
| (1) |
Since it is rare to find two different substances with identical densities, density is of value in helping to identify materials.
The specific gravity of a substance is defined as the ratio of the density of the substance to the density of water (1 gram/cm3). This ratio is a convenient physical property since it has no units and is therefore independent of the system of measure you use to determine it.
Archimedes' principle states that the buoyant force experienced by a submerged object is equal to the weight of the liquid displaced by the object. Experimentally this appears in the fact that the submerged object apparently weighs less by an amount equal to the weight of the liquid displaced. The buoyant force can be expressed as
| (2) |
where d is the density of the liquid, g is the acceleration of gravity and v is the volume of the immersed object (or the immersed part of the body if it floats). In this experiment the pan balances will compare masses in grams rather than weights. Since W=mg, the apparent change in mass when submerged is
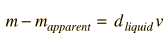 | (3) |
Archimedes' principle will be used to determine the volume of an object by submerging it in a liquid of known density.
| Procedure |
|
|
I. Determination of metal density by direct measurement of volume and mass.
- Using the pan balance, determine and record the mass of the metal cylinder provided.
- Use the vernier caliper to measure the length and diameter of the cylinder. Determine the volume in cm^3.
- Calculate the density of the metal.
Archimedes' principle will be used in this experiment to determine the volume of an object by submerging it in a liquid of known density.
Procedure
I. Determination of metal density by direct measurement of volume and mass.
- Using the pan balance, determine and record the mass of the metal cylinder provided.
- Use the vernier caliper to measure the length and diameter of the cylinder. Determine the volume in cm3.
- Calculate the density of the metal.
II. Holding the string, lower the metal into the water until it is completely submerged. Record the new water level.
Determine the volume of the metal and recalculate the density using this volume and the mass from part I.
III. Testing of Archimedes' principle with metal sample.
1. Make use of the movable platform on the pan balance to support the graduated cylinder of water. Hang the metal cylinder on the hook above the pan so that the metal is suspended and submerged in the water without touching the sides. Determine its apparent mass using the scale. Find the difference between the actual and apparent masses and compare this to the mass of the water displaced using relationship (3).
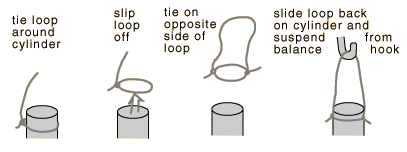
IV. Measurement of rock sample densities using Archimedes principle.
1. Two rock samples will be supplied. One is a light-colored rock typical of the material of which the continents are made, and the other is a dark basaltic rock characteristic of the ocean floors. Carefully determine the mass of each with the pan balance. This mass determination should be made while the rocks are dry- they will pick up a significant mass of water when wet.
2. Tie a light string on each sample so that they can be suspended from the hook above the pan of the balance. Fill a beaker with enough water to submerge the sample and use Archimedes principle to determine the density of each rock.
Data Sheet - Density and Buoyancy
I. Mass of metal ____________________
Length ____________________
Diameter ____________________
Volume ____________________ Density ____________________
II. Water level 1 ____________________
Water level 2 ____________________
Volume ____________________ Density ____________________
III. Apparent mass ____________________
Actual mass ____________________
Mass difference ___________ Mass of water displaced __________________
IV. Light Colored Rock
Mass ____________________
Apparent mass ____________________
Volume ____________________ Density ____________________
Dark Rock
Mass ____________________
Apparent mass ____________________
Volume ____________________ Density ____________________
Questions:
1. Why does wood float? How can a steel barge float?
2. Equal volumes of lead and aluminum are submerged in water. Which feels the greatest buoyant force? Explain.
3. Would the Archimedes principle method give accurate densities for minerals with enclosed air bubbles? Explain.
Equipment: Density and Buoyancy
|
|
Apparatus movie
Vernier caliper movie