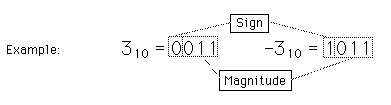
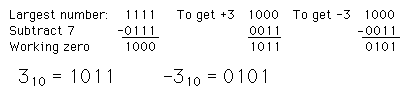Signed Integer Representations
Sign magnitude: the most significant bit is assigned to the algebraic sign.

Offset binary: subtract half the largest possible number to get the value represented. I.e., you use half the largest number as the "zero" of the scale. For four bits:
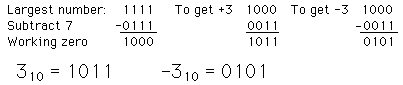
2's Complement: negative integer is the complement of the positive integer plus one.

Other Integer Representations
Binary Coded Decimal (BCD or 8421 BCD): each individual digit of the decimal number is represented by a 4-bit binary number.
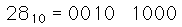
Excess-3: Add 3 to the number, then represent by 4-bit binary number.
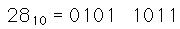
4221 Code: Four bits represent 4,2,2,1 instead of 8,4,2,1
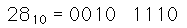
Gray Code: Starting at zero, make one change in the least significant possible bit to take you to the next state

| Number Systems |
Electronics concepts
Digital Circuits
| HyperPhysics*****Electricity and magnetism | R Nave |