First Order Non-homogeneous Differential Equation
An example of a first order linear non-homogeneous differential equation is
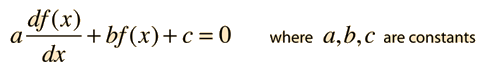
Having a non-zero value for the constant c is what makes this equation non-homogeneous, and that adds a step to the process of solution. The path to a general solution involves finding a solution to the homogeneous equation (i.e., drop off the constant c), and then finding a particular solution to the non-homogeneous equation (i.e., find any solution with the constant c left in the equation). The solution to the homogeneous equation is
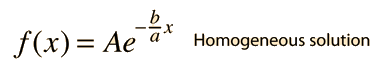
By substitution you can verify that setting the function equal to the constant value -c/b will satisfy the non-homogeneous equation.

It is the nature of differential equations that the sum of solutions is also a solution, so that a general solution can be approached by taking the sum of the two solutions above. The final requirement for the application of the solution to a physical problem is that the solution fits the physical boundary conditions of the problem. The most common situation in physical problems is that the boundary conditions are the values of the function f(x) and its derivatives when x=0. Boundary conditions are often called "initial conditions". For the first order equation, we need to specify one boundary condition. For example:
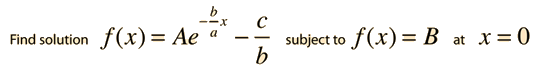
Substituting at x=0 gives:

| Example of capacitor charging |
| HyperPhysics****HyperMath*****Differential equations | R Nave |
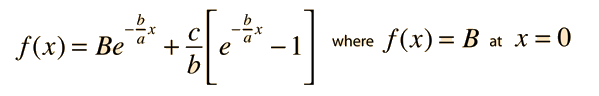 .
.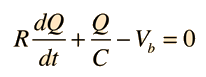 .
. .
.
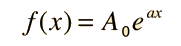 .
.
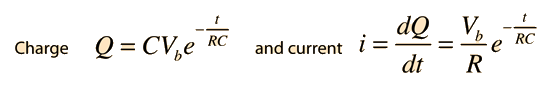 .
.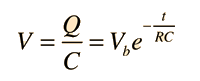 .
.