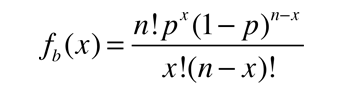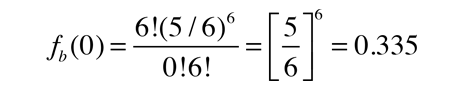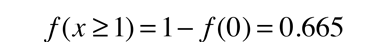Statistics of Dice Throw

The probababilities of different numbers obtained by the throw of two dice offer a good introduction to the ideas of probability. For the throw of a single die, all outcomes are equally probable. But in the throw of two dice, the different possibilities for the total of the two dice are not equally probable because there are more ways to get some numbers than others. There are six ways to get a total of 7, but only one way to get 2, so the "odds" of getting a 7 are six times those for getting "snake eyes". This simple example raises the idea of distinguishable states. For example, throwing a 3 is twice as likely as throwing a 2 because there are two distinguishable ways to get a 3.

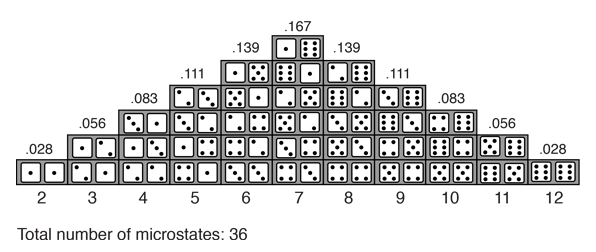
The probability of getting a given value for the total on the dice may be calculated by taking the total number of ways that value can be produced and dividing it by the total number of distinguishable outcomes. So the probability of a 7 on the dice is 1/6 because it can be produced in 6 ways out of a total of 36 possible outcomes.

Of Dice and the Binomial Distribution

The throw of a die or the picking of a card out of a deck are perhaps the most visible examples of the statistics of random events. Most of the conceptual tasks in probability for these kind of events can be handled with the binomial distribution. The binomial distribution

can serve as a kind of "multi-tool" for common statistical questions.

1. Given one throw of a die, what is the probability of throwing a 2?

   

2. What is the probability of throwing two 2's in a row?

   

3. What is the probability that in six throws of the die you will not throw any twos?

   

4. What is the probability that you will throw at least one 2 in six throws?

   

5. What is the average number of 2's that you would throw with a total of six throws of the die?

       The average number for a given outcome is the number of trials times the probability for that outcome. So the average is = np = 6(1/6) =1.

6. What is the probability that you will throw exactly one 2 in six throws?