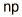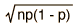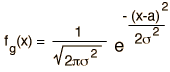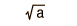Comparison of Distribution Functions

DistributionFunctional FormMeanStandard Deviation

Binomial

Gaussian

Poisson

 Index
  HyperPhysics*****HyperMath *****Algebra Go Back





Binomial Distribution Function

DistributionFunctional FormMeanStandard Deviation
Binomial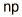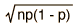

The binomial distribution function specifies the number of times (x) that an event occurs in n independent trials where p is the probability of the event occurring in a single trial. It is an exact probability distribution for any number of discrete trials. If n is very large, it may be treated as a continuous function. This yields the Gaussian distribution. If the probability p is so small that the function has significant value only for very small x, then the function can be approximated by the Poisson distribution.

If the probability of an event is p = and there are n = events, then the probability of that event being observed times is . For these conditions, the mean number of events is and the standard deviation is .

Caution!

The processor cannot handle the factorials and powers for large numbers. If you get a probability greater than one, this is an indication that part of the calculation has given up! Use of the Gaussian distribution may be necessary for large values of n.
Index

Distribution functions
  HyperPhysics*****HyperMath *****Algebra Go Back