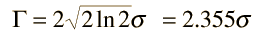Gaussian Distribution Function
| Distribution | Functional Form | Mean | Standard Deviation |
| Gaussian | 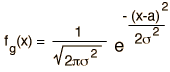 |  |  |
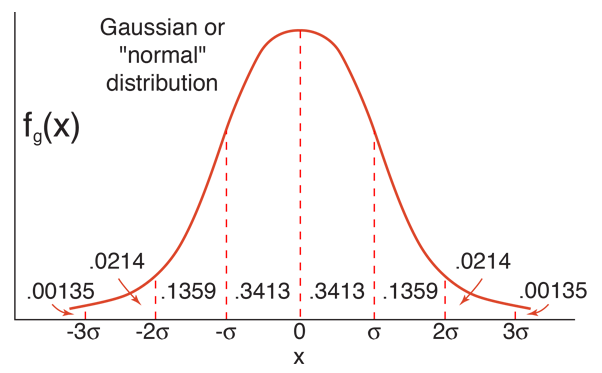
If the number of events is very large, then the Gaussian distribution function may be used to describe physical events. The Gaussian distribution is a continuous function which approximates the exact binomial distribution of events.
The Gaussian distribution shown is normalized so that the sum over all values of x gives a probability of 1. The nature of the gaussian gives a probability of 0.683 of being within one standard deviation of the mean. The mean value is a=np where n is the number of events and p the probability of any integer value of x (this expression carries over from the binomial distribution ). The standard deviation expression used is also that of the binomial distribution.
The Gaussian distribution is also commonly called the "normal distribution" and is often described as a "bell-shaped curve".
This calculation is designed for evaluation of the mean value and standard deviation and to calculate the value of the distribution function if a value x is supplied. For example, if you used it to evaluate 100 coin flips for the number of "heads", then the probability for a single coin flip would be 0.5 and the mean value of heads for 100 flips would be 50. But the standard deviation would be 5, so you should have a probability of 0.683 of having between 45 and 55 heads. The probability woulld be about 0.08 of having exactly 50 heads. But if you evaluate the value of the distribution function for values of 45 to 55 and sum them, the sum is 0.7295, so this number of events is not large enough for the Gaussian approximation to give precise results. Performing the same series of calculations using the binomial distribution yields 0.7287 so neither calculation for this size sample fits the theoretical gaussian projection.
Show Gaussian curve
Distribution functions
Applied statistics concepts
Reference
Rohlf
Sec 2-1