Zero Potential Energy
The nature of potential energy is that the zero point is arbitrary; it can be set like the origin of a coordinate system. That is not to say that it is insignificant; once the zero of potential energy is set, then every value of potential energy is measured with respect to that zero. Another way of saying it is that it is the change in potential energy which has physical significance.
When we use the simple form of the gravitational potential energy:

the assumption is usually made that the zero of gravitational potential energy is the surface of the earth and that the potential energy is proportional to the height above the earth's surface. This is an approximation which is only valid near the surface of the earth, but is fine for baseballs and other common applications of gravitational potential energy. If you are in a room, it is logical to just call the floor the zero of gravitational potential energy, and measure the energy of an elevated object with respect to the floor.
When you use the more general form of the gravitational potential energy, including the fact that it drops off with distance from the earth:
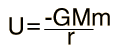
then the logic of the choice of zero potential is different. In this case we generally choose the zero of gravitational potential energy at infinity, since the gravitational force approaches zero at infinity. This is a logical way to define the zero since the potential energy with respect to a point at infinity tells us the energy with which an object is bound to the earth. This is the perspective used in calculating things like the escape velocity from the earth or other planets.
This more general case is similar to what is done with the zero of electrical potential, since is is logical to define the zero of voltage far away from any charges.
Voltage concepts
| HyperPhysics***** Mechanics | R Nave |