Lagrange Points of the Earth-Moon System
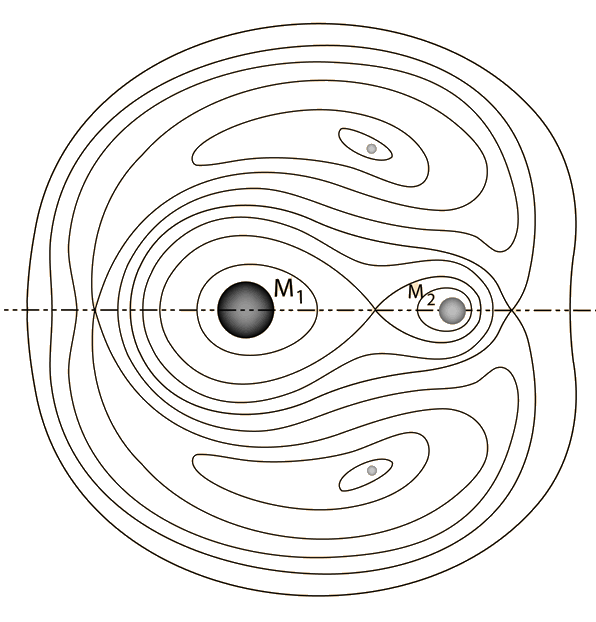
A mechanical system with three objects, say the Earth, Moon and Sun, constitutes a three-body problem. The three-body problem is famous in both mathematics and physics circles, and mathematicians in the 1950s finally managed an elegant proof that it is impossible to solve. However, approximate solutions can be very useful, particularly when the masses of the three objects differ greatly.
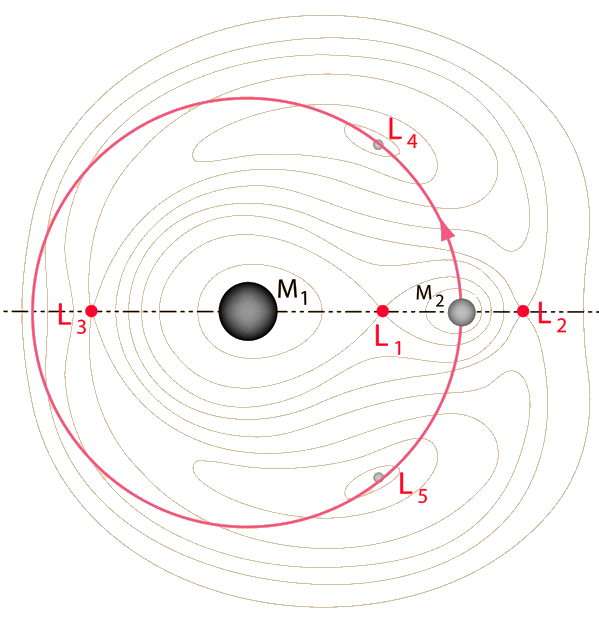
For the Sun-Earth-Moon system, the Sun's mass is so dominant that it can be treated as a fixed object and the Earth-Moon system treated as a two-body system from the point of view of a reference frame orbiting the Sun with that system. 18th century mathematicians Leonhard Euler and Joseph-Louis Lagrange discovered that there were five special points in this rotating reference frame where a gravitational equilibrium could be maintained. That is, an object placed at any one of these five points in the rotating frame would stay there, with the effective forces with respect to this frame canceling. Such an object would then orbit the Sun, maintaining the same relative position with respect to the Earth-Moon system. These five points were named Lagrange points and numbered from L1 to L5.
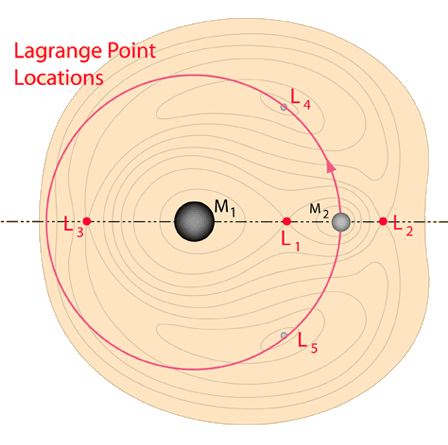 | The Lagrange points L4 and L5 constitute stable equilibrium points, so that an object placed there would be in a stable orbit with respect to the Earth and Moon. With small departures from L4 or L5, there would be an effective restoring force to bring a satellite back to the stable point. |
The L5 point was the focus of a major proposal for a colony in "The High Frontier" by Gerard K. O'Neill and a major effort was made in the 1970's to work out the engineering details for creating such a colony. There was an active "L5 Society" that promoted the ideas of O'Neill. The L4 and L5 points make equilateral triangles with the Earth and Moon.
The Lagrange points L1, L2 and L3 would not appear to be so useful because they are unstable equilibrium points. Like balancing a pencil on its point, keeping a satellite there is theoretically possible, but any perturbing influence will drive it out of equilibrium. However, in practice these Lagrange points have proven to be very useful indeed since a spacecraft can be made to execute a small orbit about one of these Lagrange points with a very small expenditure of energy. They have provided useful places to "park" a spacecraft for observations. These orbits around L1 and L2 are often called "halo orbits". L3 is on the opposite side of the Earth from the Moon, so is not so easy to use.
| Earth-Sun Lagrange Points |
Orbit concepts
Reference
Klarreich
| HyperPhysics***** Mechanics ***** Orbits | R Nave |