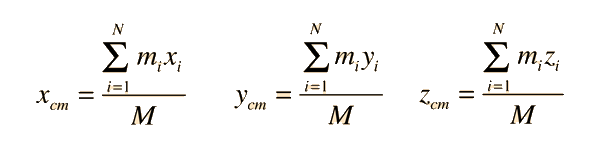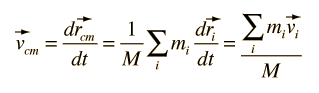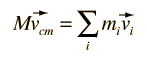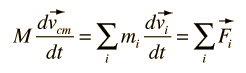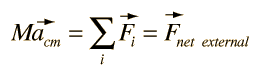Newton's Second Law for an Extended Object

The utility of Newton's second law for the description of the motion of extended objects is the key to its general practical usefulness. The motion of any real object may involve rotations as well as linear motion, but the motion of the center of mass of the object can be described by an application of Newton's second law in the following form:

Show

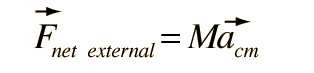If you know the net force exerted upon an object, you can predict the motion of its center of mass, even though it may be executing rotation or other internal motions.

The standard visualization examples for this application are:

• A ballistic trajectory of a rotating object - the center of mass of an extended object that is rotating will follow the same trajectory that a point mass would follow after it is launched.
• A set of masses connected by springs will follow a path such that its center of mass moves along the same path that a point mass of the same total mass would follow under the influence of the same net force.
• Combining the features of the two examples above, a pair of masses connected by a spring could be launched into a ballistic trajectory with both rotation and oscillation with respect to the center of mass. Even with this complicated internal motion, the center of mass will follow the same simple ballistic trajectory that a point mass would follow with the same launch velocity.
• If an artillery shell in a ballistic trajectory explodes in mid-flight, then in the absence of air friction, the center of mass of the fragments would hit at the same point that the intact shell was targeted.

Newton's Second Law for a System of Particles

The form of Newton's second law for a system of particles will be developed with the understanding that the result will apply to any extended object where the particles are in face connected to each other.

The center of mass of a system of particles can be determined from their masses and locations.

This center of mass can be located by a position vector:

The velocity of the center of mass can be obtained by taking the derivative of the position vector.

Rearranging this shows that the total momentum of the system of particles is just the total mass times the velocity of the center of mass.

Then taking the derivative of this expression gives

where F_i is the vector force on the i^th particle. This can be rearranged to the form

Since nothing we have done addressed whether the particles are connected or not, this result generally applies to a system of discrete particles or to an extended object consisting of connected mass elements.