Vertical Trajectory
Objects moving at high speeds through air encounter air drag proportional to the square of the velocity. Describing the motion of objects under this quadratic drag usually requires numerical techniques rather than straight analytic formuli since the drag force and the gravitational force are not acting along the same line. The case of the vertical trajectory can be treated analytically since the forces are colinear. It is common practice to express the velocity and time in terms of the terminal velocity vt and a characteristic time τ. The characteristic time is defined as the terminal velocity divided by the acceleration of gravity, τ = vt/g.

Two common approaches to the quadratic drag force are:
1. Express the drag in terms of a single drag coefficient c:
| 2. Assume that drag is proportional to cross-sectional area and express in terms of area and a shape-dependent drag coefficient C: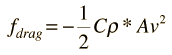
|
Fluid friction
| HyperPhysics***** Mechanics ***** Fluids | R Nave |