Mean Lifetime for Particle Decay
The decay of particles is commonly expressed in terms of half-life, decay constant, or mean lifetime. The probability for decay can be expressed as a distribution function

To normalize this distribution function:
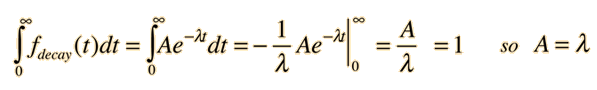
The probability that a given particle will decay within time t is given by the integral of the decay distribution function from 0 to t. This is not the quantity which we wish to calculate - we want the average time the particle will exist without decaying. The probability that a particle is not decayed is one minus the probability that it will decay. The probability that a particle will remain at time t is then:
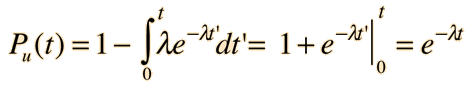
The average survival time is then the mean value of time using this probability function.

This integral may be evaluated by integration by parts. It is made slightly more direct by the substitution x = λt:
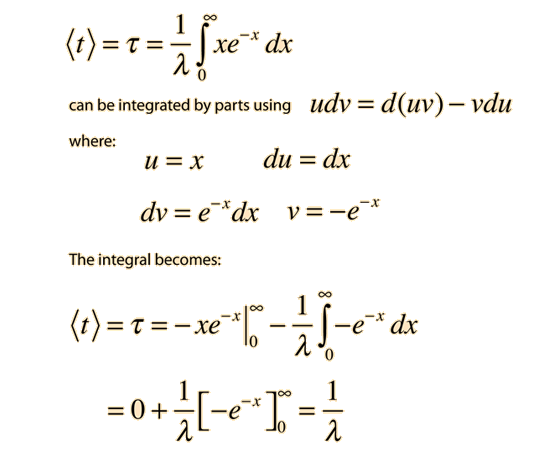
So the mean lifetime for particle decay is given by
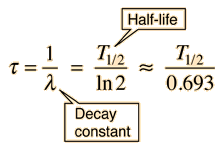
Any quantity A which depends upon this decay can then be expressed as
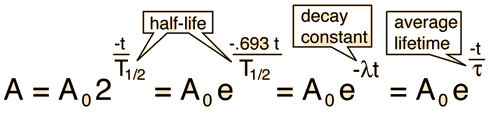 |
|
| Graph of decay | Calculation |
| HyperPhysics***** Nuclear | R Nave |