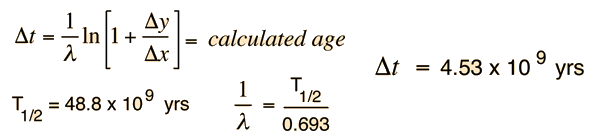Radioactive Dating
Because the radioactive half-life of a given radioisotope is not affected by temperature, physical or chemical state, or any other influence of the environment outside the nucleus save direct particle interactions with the nucleus, then radioactive samples continue to decay at a predictable rate and can be used as a clock. This makes several types of radioactive dating feasible. For geologic dating, where the time span is on the order of the age of the earth and the methods use the clocks in the rocks, there are two main uncertainties in the dating process:
- What was the amount of the daughter element when the rocks were formed?
- Have any of the parent or daughter atoms been added or removed during the process?
Starting with the simplest case where there are no daughter atoms present and no mass is lost from the sample, the age can be determined by measuring the relative amounts of the isotopes. This can be done by chemical means, but for precise determinations, mass spectrometry can be used. From the radioactive decay equations, an expression for elapsed time can be developed. Using the common nuclear practice of calling the isotopes "parent" and "daughter", we use P and D to indicate the associated numbers of atoms. The requirement of keeping the same number of nuclei gives
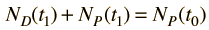
and the radioactive decay relationship is
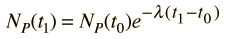
The elapsed time is then

but with the use of the first expression above can be expressed in terms of the present concentrations of the parent and daughter isotopes.

Now suppose that there was an original amount of the daughter element present at the formation time of the sample being studied. This adds an additional unknown in the process, and requires an additional piece of data to permit a solution for elapsed time. The requirement on the populations is now

Fortunately for radioactive dating processes, additional information is available in the form of other isotopes of the elements involved in the radioactive process. If there is another isotope of the daugther element D' which is presumed to be constant throughout the process, then the population requirement can be expressed in terms of the ratios

We can be reasonably confident that the isotope D' is contant if it is not radioactive (not part of one of the natural radioactive series). Using the radioactive decay equation as above, this becomes

We still have too many unknowns to solve directly for the age, but it is a reasonable presumption that all the minerals which crystallize together should show identical ages and identical isotopic ratios ND/ND'. We can then plot the ratio y = ND(t1)/ND'(t1) against x = NP(t1)/ND'(t1) for a number of minerals in a given crystalline sample and take the slope of the line. Such a line is called an isochron since all the different minerals are presumed to have crystallized together and therefore have the same age since solidification. The age can then be calculated from that slope as follows:

This calculation is expressed in terms of the decay constant λ, which is related to the half-life of the isotope.
| Example |
Reference
Krane
Sec 6.7
| HyperPhysics***** Nuclear | R Nave |