Muon Velocity
On top of a mountain at 6000 ft a muon detector measures a flux of 550 muons per hour. At a laboratory at the base of the mountain at 2000 ft, a simultaneous experiment measures 422 muons/hr. The half-life of the muon is 1.56 microseconds. How fast were the muons traveling?
Solution: First we will proceed without regard to relativity and the Lorentz transformation.
The distance traveled L=4000 ft x 0.3048 m/ft = 1219 m
The time is then calculated for the two populations as an exponential decay process using the half-life measured in the laboratory.

The results of this calculation are:
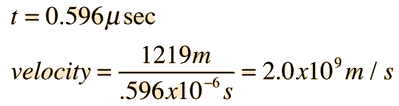 | But this can't be right! This is 6.7 times the speed of light! |
Having run into a serious violation of the speed limit of the universe on the first try, we shall attempt to include relativity in the calculation.
Considering time dilation, we must take into account that the average lifetime must be transformed by the Lorentz transformation.
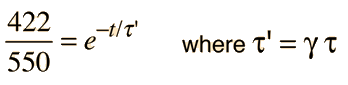
The problem with this is that there are two unknowns: we know neither the time nor the average lifetime. However, we can get a reasonable estimate of the average lifetime by assuming that the velocity is essentially =c. We use this assumption to calculate the time of transit.
