Damping of Levitated Magnet Motion
A small rare-earth magnet is suspended above a yttrium based superconductor when the Magnetic field is actively excluded from the superconductor (Meissner effect). The tiny magnet can be caused to spin by tapping it with a small instrument such as the tip of tweezers. Even though the magnet is continuously suspended, this rotational motion is damped. The rotation will slow down and it will go into a rocking mode and finally come to rest.
 | The magnet is suspended over the superconductor by immersing the superconducting disc in liquid nitrogen (77K). The induced currents in the superconductor mirror the poles of the magnet and adjust so quickly that the magnet can be translated or rotated and remain suspended. |

The damping of the oscillatory motion of the levitated magnet was investigated by taking digital video of the motion and converting it to a Quicktime movie. Measurements from the Quicktime movie were made at 1/30 sec intervals using VideoPoint. The data was transferred to an Excel spreadsheet to make the plots. For a first approximation, the motion could be modeled as a damped sine wave:
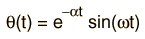
Analysis of the damping in the illustration above gives a damping coefficient of 0.247. This number was obtained by doing a least-squares fit of the peaks of the damped oscillation. Closer examination reveals that the period of the damped motion is changing, as illustrated below.
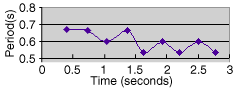 | The period of the damped motion clearly decreased with time, decreasing from about 0.68 to 0.55 s in about 3 seconds. The data plotted at left was based on the peak measurements and no extrapolation was done, so the data is rather rough. The decrease in period appears to be almost linear with time if the oscillations in the period are taken to be measurement artifacts. |
A number of interesting questions are raised by this experiment. First of all, "What is the origin of the damping?" and then "Why does the period of the oscillation change with time?". The magnet was suspended over the black yttrium-based superconducting disc with no other surrounding metals, so if the damping is from eddy currents, these currents must be in the magnet itself. The currents in the superconductor itself should not represent any loss in energy. If the frequency of oscillation were dependent solely upon the mass and size of the magnet, then you would not observe any change in period with amplitude. Non-linearity in the restoring forces causing the oscillations suggests that they too are dependent upon eddy currents in the magnet. Suggestions about modeling the damping and period change would be welcomed.
Superconductivity concepts
| HyperPhysics***** Condensed Matter | R Nave |