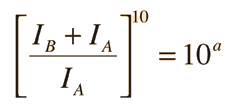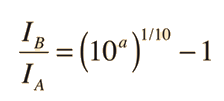Masking

This statement carries the essentials of the conventional wisdom about sound masking. Low-frequency, broad banded sounds (like water running) will mask higher frequency sounds which are softer at the listener's ear (a conversational tone from across the room). For a single frequency masking tone, masking curves can be determined experimentally. Also, from the idea of the just noticeable difference in sound intensity, one can approximately calculate the amount of a added second sound that would exceed the jnd and thus be audible.

Broadband white noise tends to mask all frequencies, and is approximately linear in that masking. By linear you mean that if you raise the white noise by 10 dB, you have to raise everything else 10 dB to hear it.

Masking Curves

Shown are the masking effects of 1200 Hz tones of various intensities. Note that it is effective in masking sounds above it in frequency, but not below. The dips at 1200 and 2400 come from the effects of beats, which make the masked tone easier to detect.

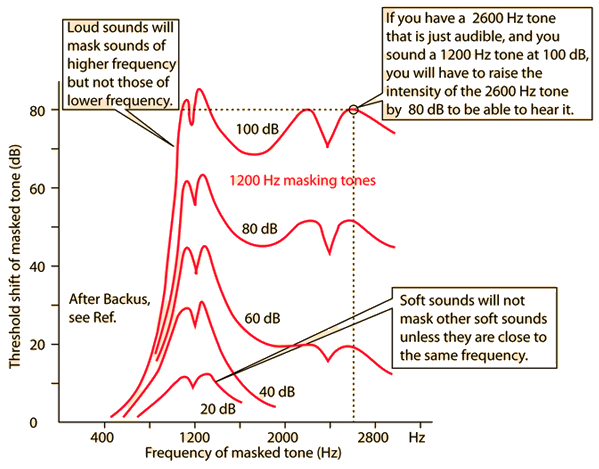
Backus credits this data to Harvey Fletcher in "Speech and Hearing in Communication", p155"

Although masking is a complex phenomena, the experience of masking of higher frequency sounds by strong low frequency sounds is common experience and of considerable significance to orchestration. It is easy to create circumstances where a strong bass brass section can mask the softer, higher frequency sounds of the woodwind section.

Audibility Threshold, Second Sound

If the general Just Noticeable Difference for sound intensity is taken to be one decibel, then the addition of a second sound would have to raise the total intensity by 1 dB to be heard. This is roughly a 25% increase, so the second sound would have to have about 1/4 the intensity, or about 6 dB less than the existing, masking sound. While this approach is not an adequate treatment of the complex subject of masking, it does permit a calculation of the amount of a second sound required to meet any criterion which is stated in terms of the decibel increase in the sound field.

The real test of any model is its comparison with experiment, and if you compare this calculation with the experimental curves for masking by pure tones above, you will find that it does not agree well. One of the things this suggests is that using a 1 dB increase in overall sound field intensity as the just noticeable difference is an oversimplification. In fact, it tells you that you should be quite wary of using the 1 dB JND at all except for the assessment of how much you should increase the dB level of the same sound to produce an audible difference.

Calculation Details, Masking Threshold

If the amount of sound B which must be added to pre-existing sound A must increase the overall decibel level by an amount a in decibels, that requirement can be stated as

Solving for the ratio of the two intensities

This ratio in decibels can be subtracted from the level I_A in dB to get the threshold for I_B which could just be heard.