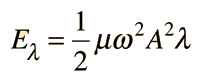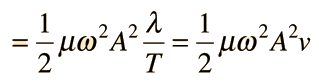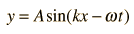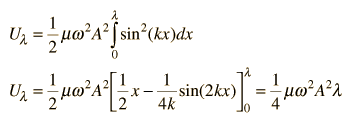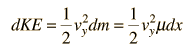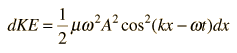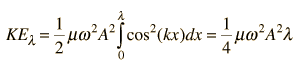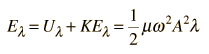Energy in a String Wave
The energy associated with a traveling wave in a stretched string is conveniently expressed as the energy per wavelength.
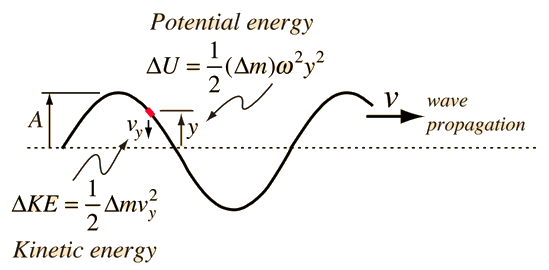
The energy of a small segment of the string can be expressed as the sum of the kinetic energy and elastic potential energy of the segment. The differential form of the elastic potential energy is

Using the description of a traveling wave
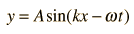
the potential energy expression becomes

The energy for a full wavelength can be found by integrating this expression at a given time, and it is most convenient to set t=0 for this integration. The energy for one wavelength along the string is
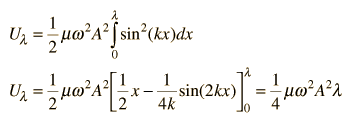
The differential kinetic energy is
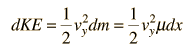
Using the velocity expression

the kinetic energy takes the form
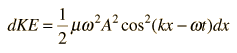
and again setting t=0 for simplification
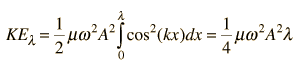
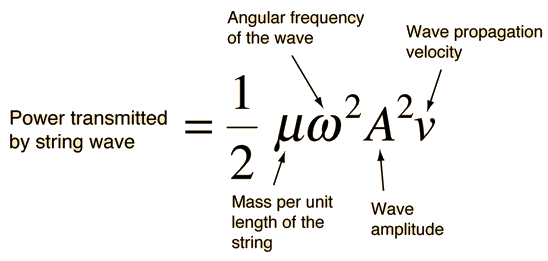
The total energy associated with a wavelength is
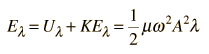
Since this amount of energy is transported a distance of one wavelength along the string in one period, this expression can be used to calculate the power transmitted along a string.
Both potential energy and kinetic energy minimum at peak of wave?
A much-discussed example of energy in string waves is the situation where at the peak of a traveling sinusoidal string wave both the kinetic energy and potential energy are minimum. See Halliday, Resnick & Walker or the Stack Exchange discussion.
The situation of a traveling wave moving along the string is energetically different from the statically displaced string. For a static stretched string, the straight configuration is one of minimum potential energy. It takes work to displace the string perpendicularly, and results in a longer string which increases the tension. So the displaced string has a higher potential energy.
The unique point in the case of the traveling wave in the string is the element of the string that is at the maximum displacement as the wave passes. That element has a zero instantaneous velocity perpendicular to the straight string configuration, and as the wave goes "over the hump", it also has minimum tension. So that element of the string has the minimum energy compared to other elements along the sinusoidal contour. This does not imply that a wavelength of the sinusoidally contoured string has less potential energy than the straight string. The sinusoidally contoured string is longer than a wavelength of straight string and will have greater elastic potential energy. As that sinusoidal contour moves along the string, it transports energy.
|