Ocean Waves
The velocity of idealized traveling waves on the ocean is wavelength dependent and for shallow enough depths, it also depends upon the depth of the water. The wave speed relationship is
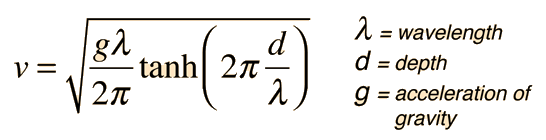
| Calculation |

Any such simplified treatment of ocean waves is going to be inadequate to describe the complexity of the subject. It is certainly a subject that has been studied thoroughly, but no single model is going to apply to all cases. Some of the things that have been learned will be summarized here.
It will be presumed that ocean waves obey the basic wave relationship c=fλ , where c is traditionally used for the wave speed or "celerity". The term celerity means the speed of the progressing wave with respect to stationary water - so any current or other net water velocity would be added to it.
The shape of an ocean wave is often depicted as a sine wave, but the the experimental waveshape is described as a "trochoid". A trochoid can be defined as the curve traced out by a point on a circle as the circle is rolled along a line. The following sketch is adapted from Bascom.
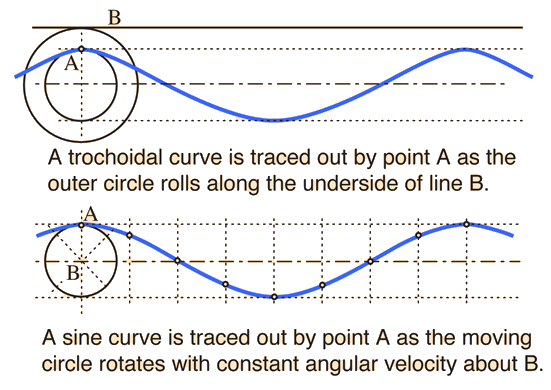
The trochoid shape does approach the sine curve in shape for small amplitudes, but you can perhaps see that the shape is different, with a narrowing of the peaks of the trochoid compared to the sinusoid. This narrowing or steepening of the peak becomes more pronounced as the wave amplitude increases.
The discovery of the trochoidal shape came from the observation that particles in the water would execute a circular motion as a wave passed without significant net advance in their position. The motion of the water is forward as the peak of the wave passes, but backward as the trough of the wave passes, arriving again at the same position when the next peak arrives. (Actually, experiments show a slight advance of the water with the waves, but that advance is small compared to the overall circular motion.)
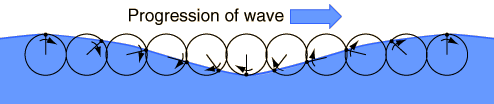
The illustration above, adapted from von Arx, shows the direction of the water motion at different points along the wave.
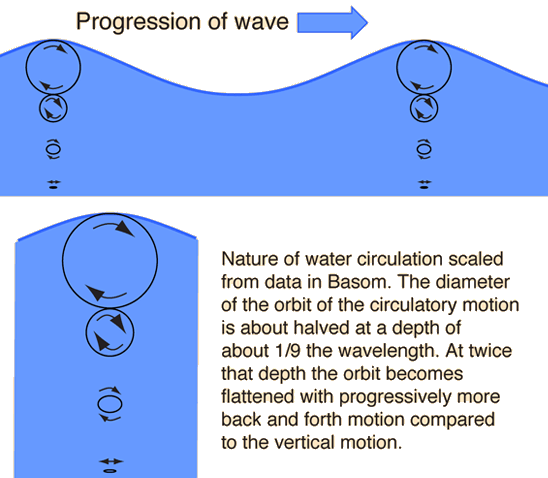
Bascom describes wavetank experiments where the circulation of the water was studied. The circles summarize the total motion of the medium when a full wavelength passes. It was common practice to inject droplets of oil which were whitened with zinc oxide and adjusted to have the same density as the water. The orbits could then be traced out on the sides of the wavetank. It was found that there was a small progression of the orbits in the direction of the wave propagation.
The fact that the water motion at depth flattens into a forward and backward surge is readily observed by scuba divers on shallow reefs. The effect of waves traveling overhead is translated into forward and backward motion of a diver suspended over the reef, and can be seen in the motion of soft corals and vegetation.
All of the description of waves above applies to long-wavelength waves which von Arx calls "gravity waves", implying that they are mainly controlled by gravity and inertia. Their wave speeds increase with wavelength, a behavior that is called "normal dispersion". For waves shorter than 1.73 cm, the surface tension of the water exerts a controlling force and von Arx calls them "capillary waves". Their speed increases as the wavelength gets shorter, a behavior that is called "anomalous dispersion". The minimum wavespeed at wavelength 1.73 cm is 23.1 cm/s. The following dependence of deep-water speed on wavelength is adapted from von Arx.
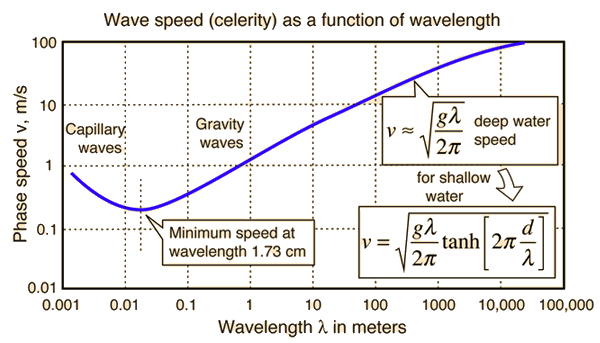
The small ripples or capillary waves are observed first when a fresh wind blows over smooth water. They have rounded crests and v-shaped troughs. Von Arx describes these waves as the way the wind gets a "grip" on the water since they are numerous and move slowly before the wind. Stories are told of seafarers who first observed these capillary waves when the wind was rising and later experienced the swells of the gravity waves, so it was thought that the capillary waves were the first mechanism by which the wind gave energy to the water. As the gravity waves build up, their wavelength tends to lengthen and speed increase until it matches the speed of the wind, at which point they can no longer extract energy from the wind.
The trochoid form that is attributed to ocean waves changes shape as the amplitude increases for a given wavelength.
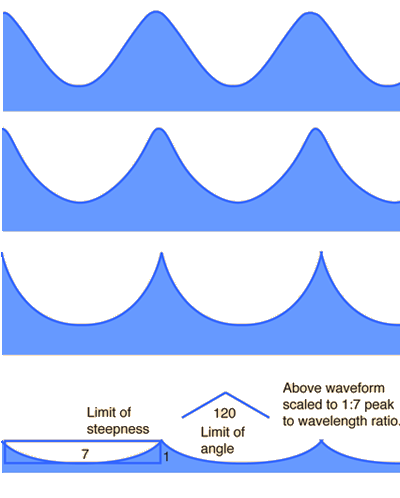 Trochoid wave models | The shape change is illustrated at left for a single wavelength, but the peak tends to become narrower and steeper as the amplitude increases for a given wavelength. Bascom reports experimental evidence from wavetanks that suggests that a ratio of 1:7 for peak height to wavelength is the maximum and that an angle of 120° is the minimum angle for a peak. Above this ratio the peaks became unstable. The bottom wave sketch is scaled to that 1:7 ratio of peak-to-trough distance compared to wavelength. |

|
As waves move toward a beach, the shallower water decreases the wavespeed, so the wavelength becomes shorter and the peak heights increase. The wavepeaks become unstable and, moving faster than the water below, they break forward. |
| Highest ocean waves | Tsunami |
Traveling Wave Concepts
References
Mayo
Bascom
von Arx
| HyperPhysics***** Mechanics | R Nave |