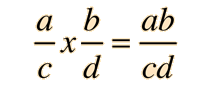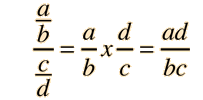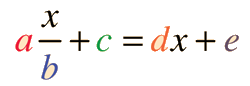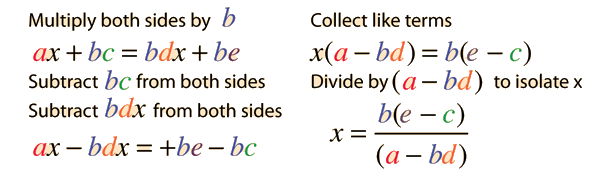Algebra Practice Equation
Solving a basic algebraic equation involves repeated applications of the golden rule of algebra to isolate the unknown quantity on one side of the equation. Using x as the unknown and other letters to represent known quantities, consider the following example equation:
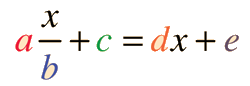
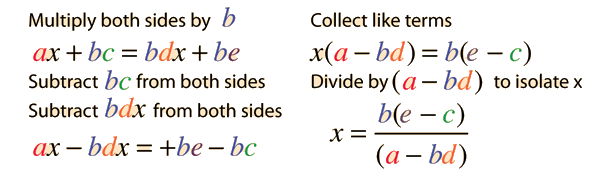
Note that there are a number of circumstances where a solution does not exist. If b=0, then the first term is infinite, so the calculation defaults to the value b=1 if no value of b is entered in order to avoid this condition for an infinity. Any set of values for which a=bd will also give an infinity, as can be seen from the expression for x above.
|
Index |