Differential Form
As a precursor to carrying out calculus operations such as derivatives and integrals, a mathematical expression will have to be placed in the differential form for the application of the methods of continuous variables. For example, a finite difference expression occurs in the development of the relationship for radioactive decay:
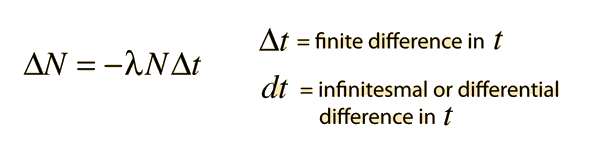
It is standard practice to use the Greek letter Δ to represent a finite difference. Often the finite difference relationship is only approximately true and is exactly true only in the limit where the differences become infinitesmally small. In this limit, the time interval Δt becomes vanishingly small and as a result, the number of decays N also becomes vanishingly small. The Δ is replaced by the differential symbol d and the resulting form
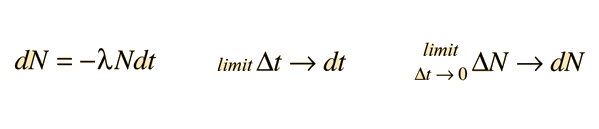
is said to be the differential form of the expression.
| HyperPhysics*****HyperMath*****Calculus | R Nave |