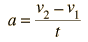Uniformly Accelerated Motion

The Freely Falling Object

INTRODUCTION

An object that is acted upon by a force which is constant in magnitude and direction will be accelerated with constant acceleration in the direction of the force. This is expressed by the relationship

Calculation

(1)

where F represents force, a is the acceleration, and m is the mass of the object.

Aristotle and other ancient philosophers reasoned (mistakenly) that the heavier a body is, the faster it should fall. Galileo is credited with discovering that the force of gravity is the cause of weight and that all bodies, regardless of their mass, are accelerated by the force of gravity at the same rate. That is, the ratio

is the same for all objects and is known as the gravitational acceleration "g".

EXPERIMENT TO BE PERFORMED

Strictly speaking, free-fall experiments must be conducted in a vacuum so that the force of air resistance does not affect the results. For relatively small, smooth objects of considerable density, however, the error introduced by conducting such experiments in the atmosphere is quite small.

For the description of the motion of an object, the variables distance, velocity, acceleration and time are involved. One way to describe the motion of an object is with the relationship

(3)

where s is the distance traveled in time t and vavg is the average velocity for the time interval t.

If the object accelerates uniformly as a result of the application of a constant force such as gravity, the acceleration can be found as the rate of change of the velocities over successive intervals of time. If equal time intervals t are used then the acceleration can be expressed as

(4)

where v2 and v1 are the average velocities over any two successive time intervals t. In this experiment the acceleration of gravity, g, will be determined directly from the motion of a freely falling object using equations 3 and 4.

APPARATUS

The free-fall apparatus has an electromagnet to hold the object until the record of its fall is to be made. When the switch to the coils of the electromagnet is opened, the magnet can no longer hold the object, and it falls freely into a cup below. A sparking device of known frequency (60 Hz) passes each spark from an outer wire through a conducting metal ring on the object, through a waxed recording tape, and on to a second wire to complete the circuit. The passage of the spark through the waxed tape leaves a small mark or spot on the tape, marking the position of the falling object. With 60 sparks per second, the space between successive marks represents the distance that the object has fallen in 1/60 second. Since the object is accelerating, the distance between marks should increase.

You will be provided with a tape from the free-fall apparatus. (A demonstration will be conducted so that you can see how the tape was made.)

PROCEDURE

1. Secure the ends of the tape to the table with masking tape.

2. Look at the dots on the tape and note the way the distance between dots increases. You should be able to detect a "misfire" of the apparatus if a dot is missing or if there is an extra mark. If a dot is missing, you need to take that into account in entering your data into the calculation program described below.

3. Find a dot for a starting point by dropping down at least a centimeter from the first marks so that the falling object will have cleared the magnetic field influence. Label this dot zero (0) and measure the distance from this zero point to each successive dot, measuring as many as possible (at least a dozen). Please note that the distance to be measured is the total distance to each dot from the starting point (zero) and not the distance from the preceding dot. This procedure improves the accuracy of the set of measurements. These distance measurements are critical since they are multiplied by a large number in calculating the acceleration. Measure the distances to the nearest millimeter and then estimate to the nearest tenth of a millimeter. Place the meter stick on its edge so that the scale is next to the paper tape and look perpendicular to the meter stick when taking your reading. You may wish to tape the meter stick down to make sure it doesn't move between measurements.

4. A Spreadsheet is an excellent tool for repetitive calculations and the plotting of data. A template titled FreefallTemplate has been set up, and you can find it under the Apple menu (extreme top left of screen). Open that template and record your measured positions in it. The template should appear similar to the illustration below. Record your position data in the column titled "Distance". The Time columns are set up to reflect the 1/60 second interval of the spark timer. The zeros in the Avg. velocity and Acceleration columns are actually the result of formulas which depend upon the distance data which you will enter.

5. Make a plot of your Distance vs Time by clicking and holding down the mouse button in the upper left box of the first Time column a nd then dragging the mouse diagonally to select a rectangle including your time and distance data. Then release the mouse button and take the mouse up to click on the icon which looks like a magic wand over a bar graph. Then use the mouse to draw a rectangle out beside yur data table where you want the graph to appear. Follow the prompts to create a line graph of your positon data with the first column used as values for the horizontal axis.

The slope of the distance vs time graph represents the rate of change of distance, which is the velocity.

6. Repeat the process above to plot your Avg. Velocity vs Time. What does this graph tell you?

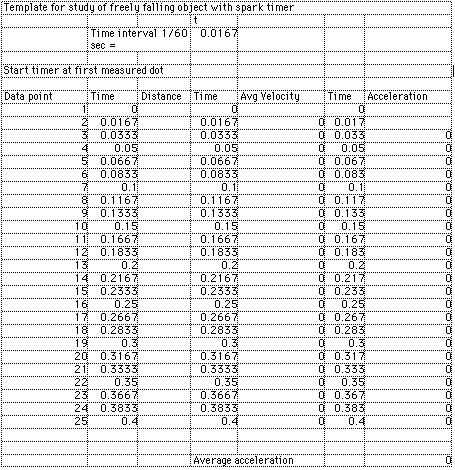
7. The values calculated for acceleration are meaningful only as far down as you have position data. Position the mouse on the first acceleration value below the level of your position data and click and hold down the mouse button. Drag the mouse down to the bottom of the column of numbers and release the mouse button to highlight these numbers. Choose Blank from the Edit menu to blank out those values. Then the calculation below should show the average acceleration in cm/s^2. (You can plot these acceleration values if you wish, but they generally swing pretty wildly because any position measurement errors are greatly magnified in the acceleration calculation.)

Graphs of position and velocity represent one good way to analyze motion, and the analysis of straight line, constant acceleration motion such as freefall provides an instructive example.