Multiplication and Division
The multiplication of complex numbers in cartesian form is binomial multiplication
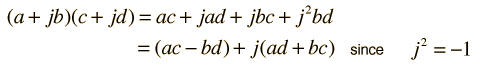
Complex numbers
| HyperPhysics****HyperMath*****Algebra | R Nave |
Multiplication and DivisionThe multiplication of complex numbers in cartesian form is binomial multiplication 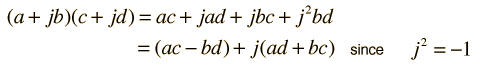 |
Index Complex numbers | ||
|
Go Back |
Rationalization of Complex NumbersThe division of complex numbers which are expressed in cartesian form is facilitated by a process called rationalization. The formation of a fraction 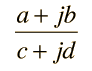 presents difficulties because of the imaginary part of the denominator. The denominator can be forced to be real by multiplying both numerator and denominator by the conjugate of the denominator. 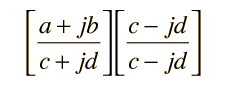 Expanding puts the result of the division in cartesian form again. 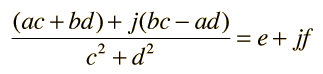 Calculation for multiplication and division |
Index Complex numbers | ||
|
Go Back |
Complex ConjugateThe conjugate of a complex number is that number with the sign of the imaginary part reversed  The utility of the conjugate is that any complex number multiplied by its complex conjugate is a real number: 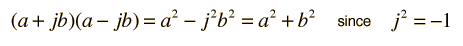 This operation has practical utility for the rationalization of complex numbers and the square root of the number times its conjugate is the magnitude of the complex number when expressed in polar form. Applications |
Index Complex numbers | ||
|
Go Back |
Applications of Complex ConjugatesWhen a real positive definite quantity is needed from a real function, the square of the function can be used. In the case of a complex function, the complex conjugate is used to accomplish that purpose. The product of a complex number and its complex conjugate is the complex number analog to squaring a real function. The complex conjugate is used in the rationalization of complex numbers and for finding the amplitude of the polar form of a complex number. One application of the complex conjugate in physics is in finding the probability in quantum mechanics. Since the wavefunction which defines the probability amplitude may be a complex function, the probability is defined in terms of the complex conjugate to obtain a real value. 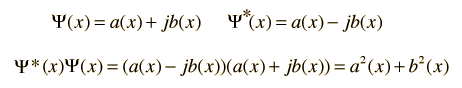 |
Index Complex numbers | ||
|
Go Back |