Gaussian Surfaces
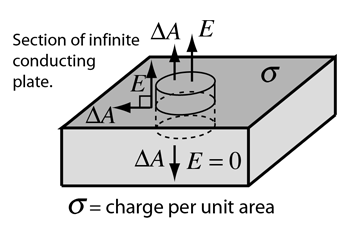
Part of the power of Gauss' law in evaluating electric fields is that it applies to any surface. It is often convenient to construct an imaginary surface called a Gaussian surface to take advantage of the symmetry of the physical situation.

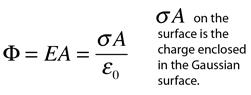
If the symmetry is such that you can find a surface on which the electric field is constant, then evaluating the electric flux can be done by just multiplying the value of the field times the area of the Gaussian surface.
| Gauss' law applications | Electric flux |
Electric field concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |