Supporting an Extended Load

For an extended system to be at equilibrium, the sum of the forces must be equal to zero and the sum of torques about any axis must equal zero. It is logical to choose one of the ends as the axis since that eliminates one of the unknown forces (lever arm = zero). Considering a long uniform wooden board, note that the mass of the board can be considered to be concentrated at its center of mass for the purposes of calculating torque. For a uniform board, the center of mass is at its geometrical center, so the lever arm with respect to either end of the board will be L/2. Choosing the left end as the axis, the torque and force equilibrium equations are shown below.

For an object of mass = kg and weight = N
which is supported by a uniform board of length = m and
mass= kg and weight = N
at distance x=m from its left end, then the torque equilibrium equation is

Weight x x + (weight of board)x Length/2 = Force#2 x Length

The force which is calculated from the torque equilibrium is
Force F2 = Newtons.
The force supporting the left end can then be calculated from the force equilibrium condition shown above and yields:
Force F1 = Newtons.
Any of the above data can be changed. When finished with editing data, click on the quantity you wish to calculate in the torque equilibrium equation. 		Index

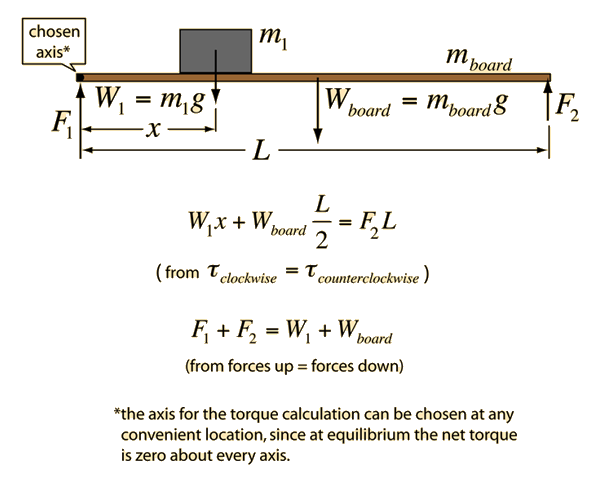
Torque equilibrium examples
 
HyperPhysics***** Mechanics R Nave
 Go Back