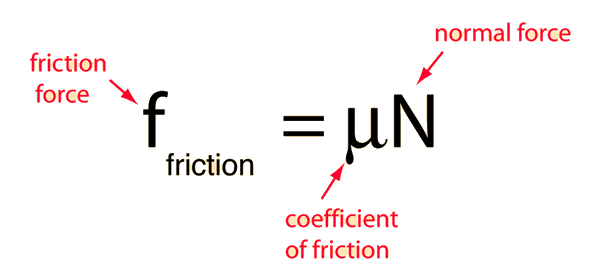
Friction and Normal Force
Part of the standard model of surface friction is the assumption that the frictional resistance force between two surfaces is proportional to the normal force pressing them together. A common exception occurs in snow where greater traction occurs by having wider tires with lower pressure. The same
normal force is exerted, but the traction (friction) is greater with the wider
tire since it doesn't pack the snow
as much. The packing of the snow tends to depend on the pressure exerted on the snow, and supporting the same weight on a smaller area implies that more pressure is exerted. This example is also an
exception to the assumption of
independence of area of contact.
With a given area of contact, increasing the normal force will pack the snow, decreasing the effective coefficient of friction.

While exceptions such as this are easily found, the assumption that friction is proportional to the normal force is still reasonably valid in many cases and forms a useful model for many circumstances.
A valid question is why does the frictional resistance increase proportionally with normal force? Jones and Childers have a thoughtful discussion of this. They point out that the area of coverage for a sliding block is actually much larger than the area of contact. Because of microscopic irregularities in the surface, the block is actually riding on a small fraction of the coverage area. Because such points of contact are deformable, an increase in normal force will actually increase the area of actual contact and increase the resistance to movement.
|
Index
Friction concepts
Reference
Jones & Childers, 2nd Ed.
Sec 4.8 |