Inclined Pulley with Friction
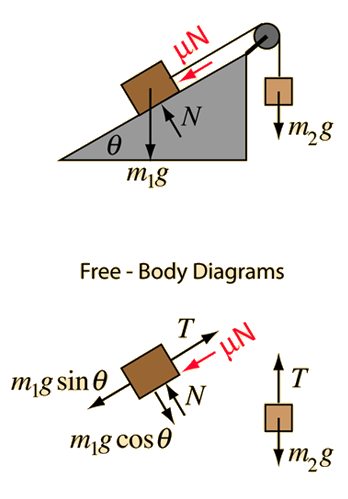 Note that the tension in the rope is NOT equal to the weight of the hanging mass except in the special case of zero acceleration. Friction must be treated with care in a situation like this. If the hanging mass is large enough to overcome friction and accelerate the mass upward on the incline, then the friction force will oppose it and act downward. If the mass on the incline is large enough, it will overcome friction and move downward, pulling the hanging mass upward. In this case the friction force will act up the incline. There is an intermediate range of masses where the block will move neither up nor down the incline. |
Application of Newton's second law to mass on incline with pulley. |
Expressions****Remove friction
Newton's laws
Standard mechanics problems
| HyperPhysics***** Mechanics ***** Newton's laws | R Nave |