Magnetic Vector Potential

The electric field E can always be expressed as the gradient of a scalar potential function

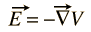
There is no general scalar potential for magnetic field B but it can be expressed as the curl of a vector function

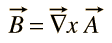
This function A is given the name "vector potential" but it is not directly associated with work the way that scalar potential is.

The vector potential is defined to be consistent with Ampere's Law and can be expressed in terms of either current i or current density j (the sources of magnetic field). In various texts this definition takes the forms

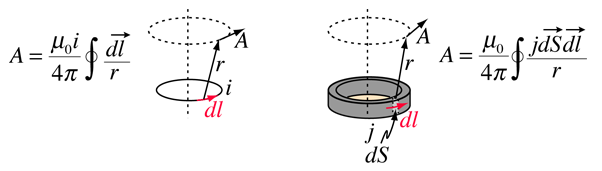
One rationale for the vector potential is that it may be easier to calculate the vector potential than to calculate the magnetic field directly from a given source current geometry. Its most common application is to antenna theory and the description of electromagnetic waves.

Since the magnetic field B is defined as the curl of A, and the by vector identity the curl of a gradient is identically zero, then any arbitrary function which can be expressed as the gradient of a scalar function may be added to A without changing the value of B obtained from it. That is, A' can be freely substituted for A where

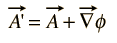
Such transformations are called gauge transformations, and there have been a number of "gauges" that have been used to advantage is specific types of calculations in electromagnetic theory.