Binomial Distribution Example
| Distribution | Functional Form | Mean | Standard Deviation |
| Binomial | 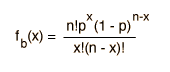 | 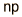 |  |
Joe throws a die six times and throws a three twice. It that incredibly lucky or unusual?
The basic probability of throwing a "3" in one throw is p=1/6 . Then for n=6 throws, the average number of 3's would be
So throwing two 3's is definitely not the expected or most probable result, but it remains to be seen how much the probability is diminished relative to the most probable result.
Now the number of ways to pick r objects out of a total of n is
which is called the permutation. But considering them to be distinguishable, this overcounts. If getting the same objects or outcomes but in different order is not going to be considered to be a different overall outcome, then we need to divide by the number of ways to arrange them, which is r! . The number of ways to pick distinguishable sets is then
which is called the combination.
The probability of getting a certain outcome r times is pr, but if you do that AND get some other outcome for the remainder of the tries (associated probability (1-p)n-r) then the probability for this combined outcome is the product of these probabilities. This is a part of the nature of general probability: the probability for any two outcomes related by a logical "AND" will be the product of the probabilities of the single outcomes. Then if the combined probability is multiplied by the number of ways to get this outcome, the result is the binomial distribution function.
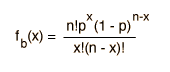
Using this function to evaluate the probabilities of 0,1,2 and 3 times for throwing a "3" by throwing a die six times gives
|
The probability for throwing a "3" twice is seen to be about half that for the expected or average value of one time. So it would not be unusual to see this happen, but it would be rarer than not throwing any 3's in six throws.
| |||||||||||||
| Comments about the form of the function |
Distribution functions
Applied statistics concepts
| HyperPhysics*****HyperMath*****Algebra | R Nave |