Stirling's Approximation for n!
When evaluating distribution functions for statistics, it is often necessary to evaluate the factorials of sizable numbers, as in the binomial distribution:
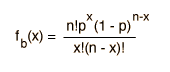
A helpful and commonly used approximate relationship for the evaluation of the factorials of large numbers is Stirling's approximation:

A slightly more accurate approximation is the following

but in most cases the difference is small. This additional term does give a way to assess whether the approximation has a large error.
Stirling's approximation is also useful for approximating the log of a factorial, which finds application in evaluation of entropy in terms of multiplicity, as in the Einstein solid. The log of n! is
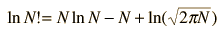
but the last term may usually be neglected so that a working approximation is

Shroeder gives a numerical evaluation of the accuracy of the approximations
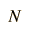 | 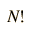 | 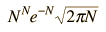 |  | 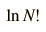 | 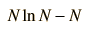 |  |
| Relation to Gamma Function |
Statistics concepts
Reference
Schroeder
App. B
Ch 2
| HyperPhysics*****HyperMath | R Nave |