Motion Graphs
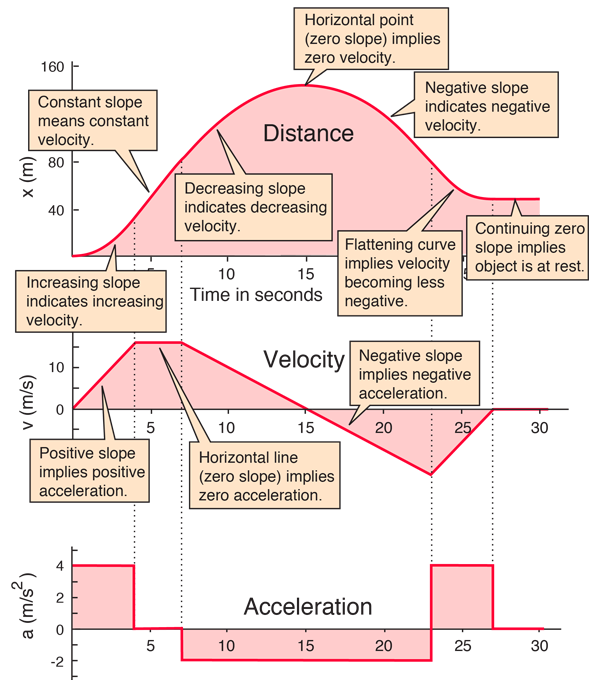
Constant acceleration motion can be characterized by motion equations and by motion graphs. The graphs of distance, velocity and acceleration as functions of time below were calculated for one-dimensional motion using the motion equations in a spreadsheet. The acceleration does change, but it is constant within a given time segment so that the constant acceleration equations can be used. For variable acceleration (i.e., continuously changing), then calculus methods must be used to calculate the motion graphs.

| Add annotation about the slopes of the graphs. |
A considerable amount of information about the motion can be obtained by examining the slope of the various graphs. The slope of the graph of position as a function of time is equal to the velocity at that time, and the slope of the graph of velocity as a function of time is equal to the acceleration.
Motion concepts
| HyperPhysics***** Mechanics | R Nave |