Velocity vs Height for Vertical Launch with Quadratic Drag

An object will be presumed to experience an air resistance force proportional to the square of its speed. If it is launched with velocity v₀ then both gravity and the force of friction act downward on it while it is traveling upward. The upward direction will be taken as positive, and the velocity as a function of height y is the object of the calculation. The expressions will be developed for the two forms of air drag which will be used for trajectories:

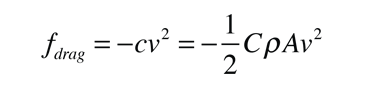
although the first steps will be done with just the form -cv² for simplicity.

The differential equation for the motion is

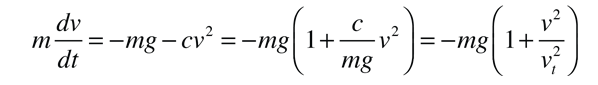
which expresses the force in terms of the terminal velocity v_t:

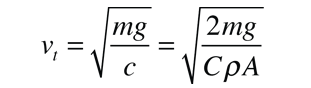
The motion equation may be converted to one in which the independent variable is distance instead of time by making use of the expression

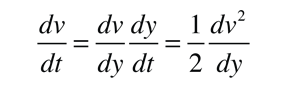
This can be used to rewrite the motion equation above as

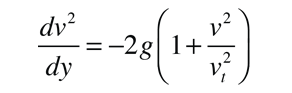
and making the substitution

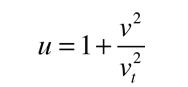
the motion equation can be written

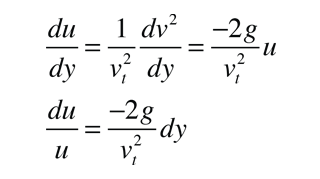
This equation can now be integrated to give

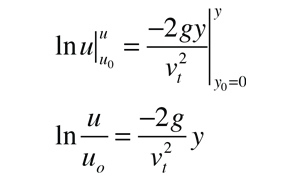
Now substituting for u and with several steps of algebraic rearrangement

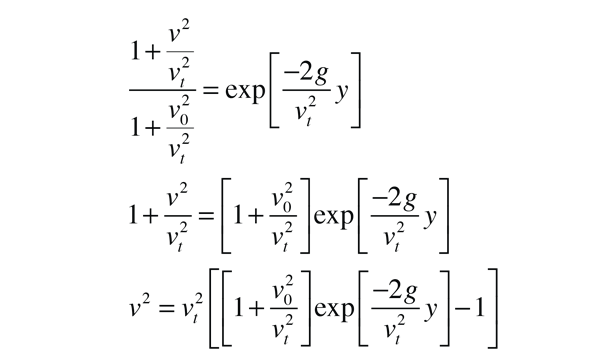
we finally arrive at an expression for the upward velocity as a function of height:

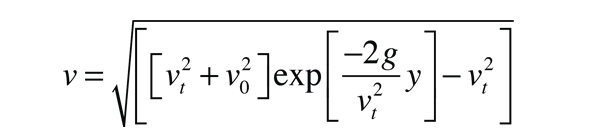
This expression only applies to the upward part of the motion, since the velocity becomes zero at that point, and upon beginning its downward motion, the drag force reverses in direction. For that part of the motion, see the freefall development.

This expression is used in the vertical trajectory calculation.