Mass on Frictionless Incline
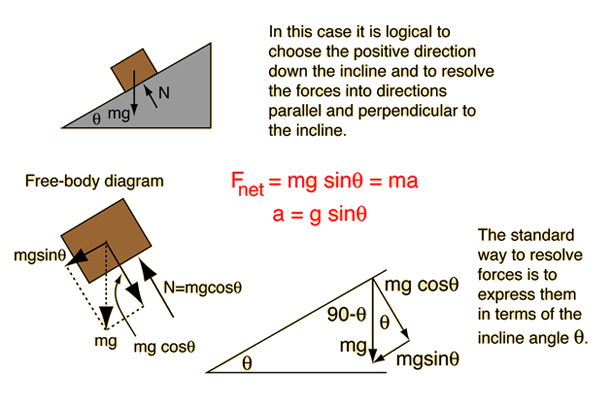
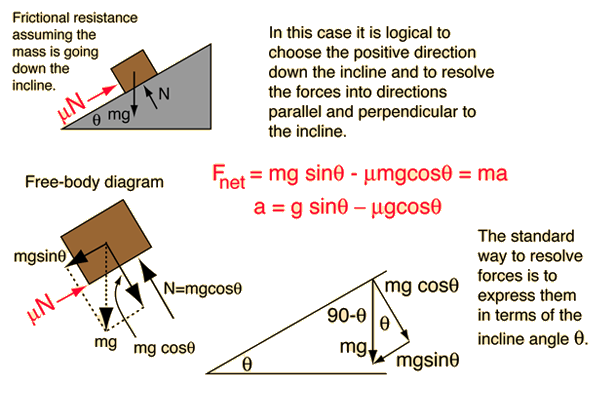
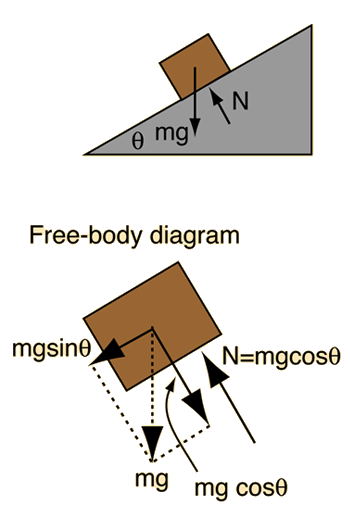
One of the insights that comes from the setup of this problem is that the force required to push a mass m up a frictionless incline is equal to mgsinθ. Checking the limiting cases, you find that it takes no force along a horizontal frictionless surface (θ=0), and a force = mg on a vertical frictionless surface (θ=90°) as you would expect.
Calculation
Add friction
Newton's laws
Standard mechanics problems
| HyperPhysics***** Mechanics | R Nave |