Lifting Mass

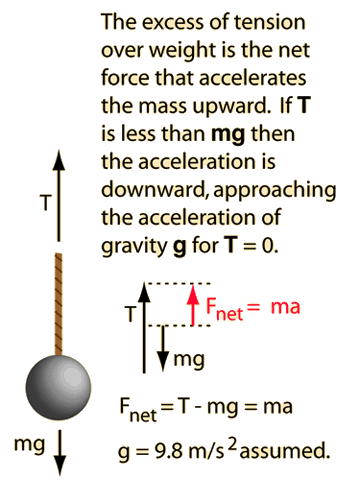
Though a straightforward application of Newton's second law, many find this problem deceptive. The common misconception which is carried into it is that the tension in the rope must equal the weight of the hanging object. When the mass is accelerated, that is not so. You may change the data and then click on either tension or acceleration in the equation below to calculate its value.

For a mass m= kg, the rope must support its weight = mg =Newtons to hold it up at rest. If the acceleration is a=m/s2 then a net force=Newtons is required to accelerate the mass. This requires a tension of T=Newtons. Note that the tension is equal to the weight only if the acceleration is zero, and that if the acceleration is negative (downward), the tension is less than the weight. If you enter a downward acceleration greater than 9.8 m/s2 you will get a negative tension, showing that you must force it downward to get an acceleration greater than that of free fall. See elevator problem