Just Temperament
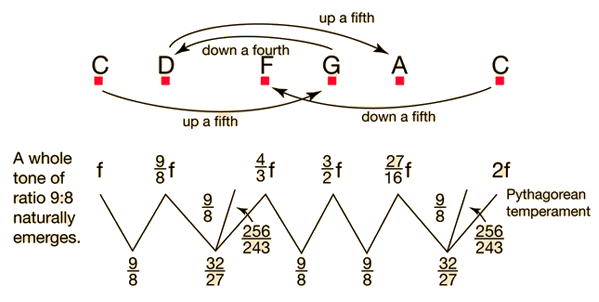
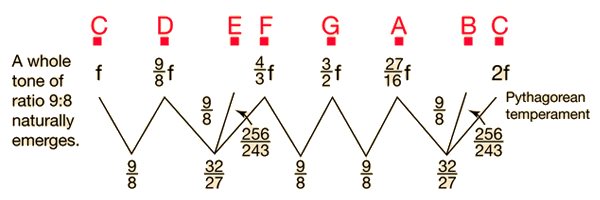
Just temperament refers to a musical scale or musical intervals which maintain exact integer ratios between pitches. For example, the ration 3:2 is said to be a "just" musical fifth and is sometimes called a "perfect fifth". Pythagorean temperament maintains just intervals for the fifth and fourth but departs for some other intervals. Equal temperament does not contain any just intervals except the octave itself. However, if five cents is taken as the just noticeable difference in pitch, the fifths and fourths of equal temperament are just within that 5¢ margin.
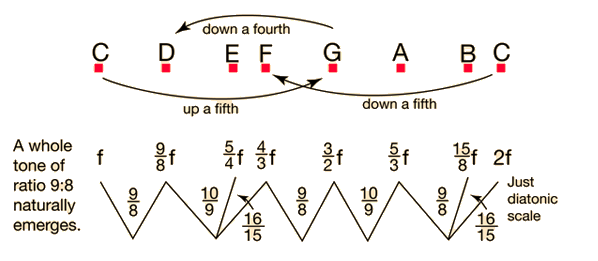
Backus makes the comment that the just diatonic scale can be build up by superimposing just major triads, and the resulting scale ensures that all the fifths and major thirds in these component triads will be just. Many difficulties arise in this scale. There are two different sized whole tones. All kinds of tone combinations are changed when you transpose to another key, so that transposition is not practical in most cases. Although Helmholtz and many others have built keyboards in just intonation, Backus' summary judgment is "the just scale has never been of any practical use".
| Harmonics are just intervals | Triads as just intervals |
Musical scales
Reference:
Backus
Ch. 8
| HyperPhysics***** Sound | R Nave |