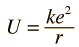Critical Ignition Temperature for Fusion
The fusion temperature obtained by setting the average thermal energy equal to the coulomb barrier gives too high a temperature because fusion can be initiated by those particles which are out on the high-energy tail of the Maxwellian distribution of particle energies. The critical ignition temperature is lowered further by the fact that some particles which have energies below the coulomb barrier can tunnel through the barrier.
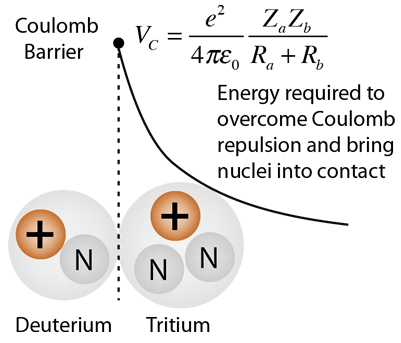
The presumed height of the coulomb barrier is based upon the distance at which the nuclear strong force could overcome the coulomb repulsion. The required temperature may be overestimated if the classical radii of the nuclei are used for this distance, since the range of the strong interaction is significantly greater than a classical proton radius.
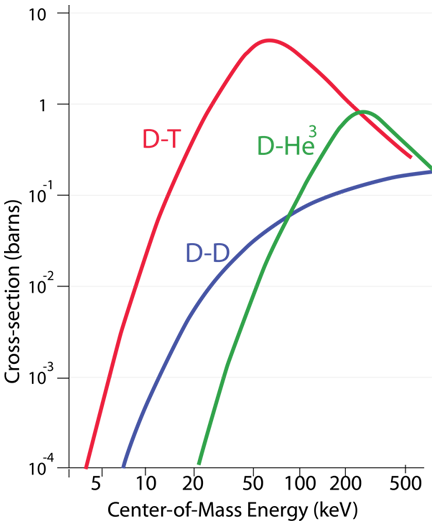
When trying to model the probability of nuclear fusion, the typical approach is to model it as a "cross-section" for the reaction to occur. This approach is perhaps more apparent in evaluating particle scattering like Rutherford scattering, but the language is often used for nuclear fusion as well. For the purposes here, cross-section can be taken to mean the probability for nuclear fusion to occur. Modeling this cross-section involves taking into account the probability for tunneling through the coulomb barrier. This probability is higher for higher energy particles, but because of the Maxwellian distribution, there are fewer of these high energy particles. Also, the effective energy of collision between the particles for fusion depends on their relative velocities, so the model calculation for nuclear fusion yield involves averaging over all relative velocities. The results of such modeling are presented as a plot of fusion cross-section as a function of average particle energy.
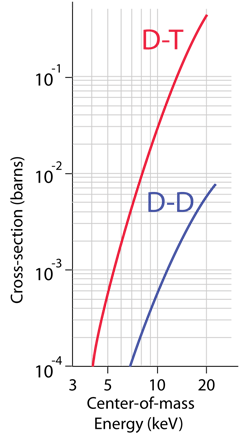 |
With all these considerations, the energy requirements for the nuclear fusion of deuterium- tritium and for deuterium-deuterium are dramatically lower than the coulomb barrier, but they are nevertheless very difficult to attain in a controlled manner.
The references suggest that the currently attainable particle energies in thermonuclear reactors is in the range 1 - 10 keV. If you just substitute those energies into the thermal energy relationship, then 1keV corresponds to a temperature of 0.77 x 107K and 10 keV corresponds to 0.77 x 108K.
|
The TFTR reached a temperature of 5.1 x 108 K, well above the critical ignition temperature for D-T fusion.
References:
Kaye & Laby
Crossfire Fusion
|
Index
Fusion concepts
References:
Krane,
Sec 14.2 |