Modeling the Probability for Proton Decay
The experimental search for proton decay was undertaken because of the implications of the grand unification theories. The lower bound for the lifetime is now projected to be on the order of τ = 1033 years. The probability for observing a proton decay can be estimated from the nature of particle decay and the application of Poisson statistics.
The number of protons N can be modeled by the decay equation

where λ = 1/t = 10-33/ year is the probability that any given proton will decay in a year. Since the decay constant λ is so small, the exponential can be represented by the first two terms of the exponential series.

For a small sample, the observation of a proton decay is infinitesmal, but suppose we consider the volume of protons represented by the Super Kameokande neutrino detector in Japan. The number of protons in the detector volume is reported by Ed Kearns of Boston University to be 7.5 x 1033 protons. For one year of observation, the number of expected proton decays is then

About 40% of the area around the detector tank is covered by photodetector tubes, and if we take that to be the nominal efficiency of detection, we expect about three observations of proton decay events per year based on a 1033 year lifetime.
So far, no convincing proton decay events have been seen. Poisson statistics provides a convenient means for assessing the implications of the absence of these observations. If we presume that a = 3 observed decays per year is the mean, then the Poisson distribution function tells us that the probability for zero observations of a decay is
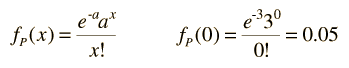
This low probability for a null result suggests that the proposed lifetime of 1033 years is too short. While this is not a realistic assessment of the probability of observations because there are a number of possible pathways for decay, it serves to illustrate in principle how even a non-observation can be used to refine a proposed lifetime.
Particle concepts
| HyperPhysics***** Quantum Physics | R Nave |