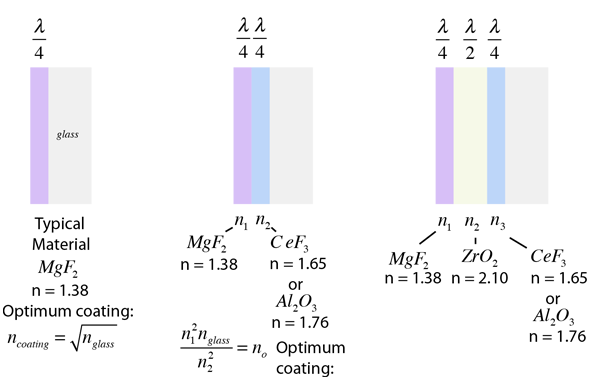Anti-Reflection Coatings
Thin film anti-reflection coatings greatly reduce the light loss in multi-element lenses by making use of phase changes and the dependence of the reflectivity on index of refraction. A single quarter-wavelength coating of optimum index can eliminate reflection at one wavelength. Multi-layer coatings can reduce the loss over the visible spectrum.
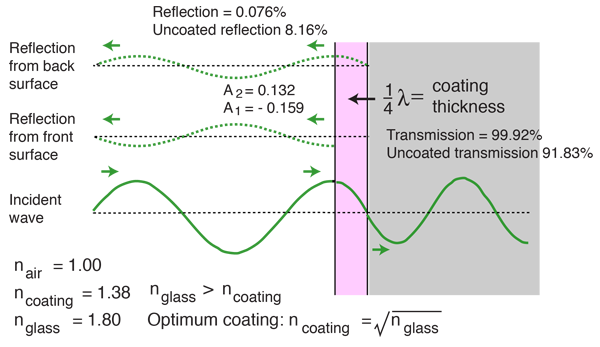
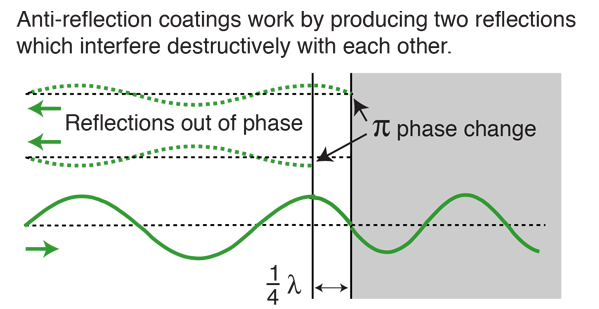
The idea behind anti-reflection coatings is that the creation of a double interface by means of a thin film gives you two reflected waves. If these waves are out of phase, they partially or totally cancel. If the coating is a quarter wavelength thickness and the coating has an index of refraction less that the glass it is coating then the two reflections are 180 degrees out of phase.
| Thin films | Example calculation |
Reflection concepts
| HyperPhysics***** Light and Vision | R Nave |