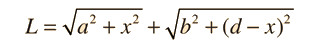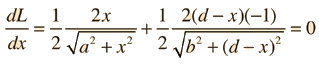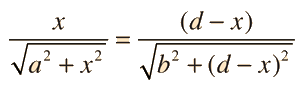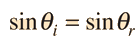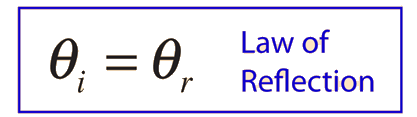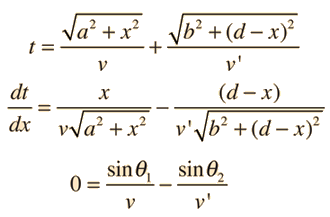Law of Reflection

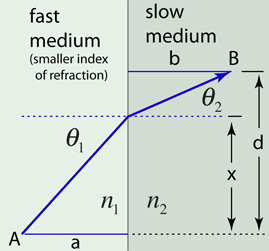
A light ray incident upon a reflective surface will be reflected at an angle equal to the incident angle. Both angles are typically measured with respect to the normal to the surface. This law of reflection can be derived from Fermat's principle.

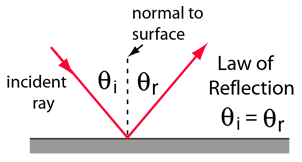The law of reflection gives the familiar reflected image in a plane mirror where the image distance behind the mirror is the same as the object distance in front of the mirror.

Fermat's Principle:Reflection

Fermat's Principle: Light follows the path of least time. Of course the straight line from A to B is the shortest time, but suppose it has a single reflection. The law of reflection can be derived from this principle as follows:

The pathlength from A to B is Since the speed is constant, the minimum time path is simply the minimum distance path. This may be found by setting the derivative of L with respect to x equal to zero.

This reduces to

which is

This derivation makes use of the calculus of maximum-minimum determination, the derivative of a square root, and the definitions of the triangle trig functions.

Fermat's Principle and Refraction

Fermat's Principle: Light follows the path of least time. Snell's Law can be derived from this by setting the derivative of the time =0. We make use of the index of refraction, defined as n=c/v.

This derivation makes use of the calculus of maximum-minimum determination and the definitions of the triangle trig functions.