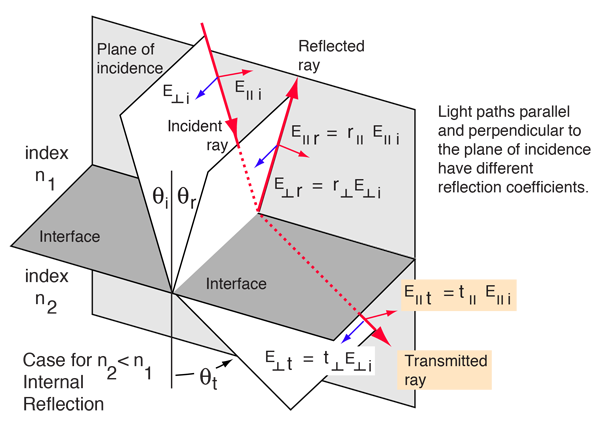
Reflection and Transmission
Internal Reflection
| Go to external reflection |
Fresnel's equations describe the reflection and transmission of electromagnetic waves at an interface. That is, they give the reflection and transmission coefficients for waves parallel and perpendicular to the plane of incidence. For a dielectric medium where Snell's Law can be used to relate the incident and transmitted angles, Fresnel's Equations can be stated in terms of the angles of incidence and transmission.
Fresnel's equations give the reflection coefficients:
 | = and | 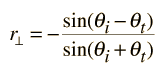 | = |
The transmission coefficients are
 | = and |
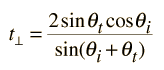 | = |
Note that these coefficients are fractional amplitudes, and must be squared to get fractional intensities for reflection and transmission.
You can choose values of parameters which will give transmission coefficients greater than 1, and that would appear to violate conservation of energy. (For example, try light incident from a medium of n1=1.5 upon a medium of n2=1.0 with an angle of incidence of 30°.) But the square of the transmission coefficient gives the transmitted energy flux per unit area (intensity), and the area of the transmitted beam is smaller in the refracted beam than in the incident beam if the index of refraction is less than that of the incident medium. When you take the intensity times the area for both the reflected and refracted beams, the total energy flux must equal that in the incident beam. For further details, see Jenkins and White.
Checking out conservation of energy in this situation leads to the relationship
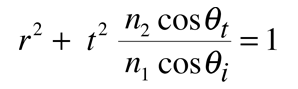
which applies to both the parallel and perpendicular cases.
Parallel case: Reflected % and transmitted %.
Perpendicular case: Reflected % and transmitted %.
| Typical curves for: | External reflection | Internal reflection |
Reflection concepts
Incident light behavior
Reference
Jenkins and White
Sec 25.2
| HyperPhysics***** Light and Vision | R Nave |