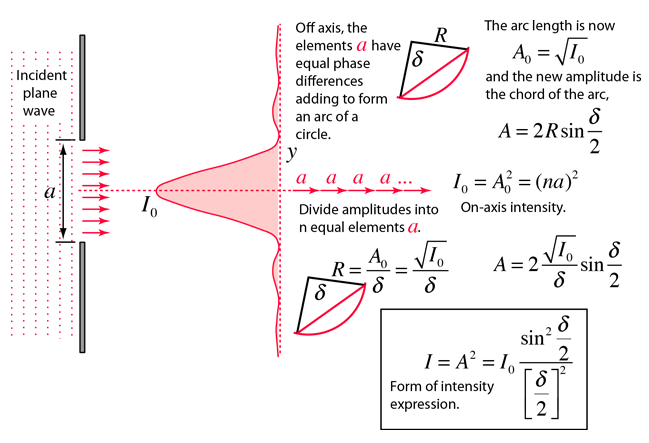
Single Slit Diffraction Intensity
Under the Fraunhofer conditions, the wave arrives at the single slit as a plane wave. Divided into segments, each of which can be regarded as a point source, the amplitudes of the segments will have a constant phase displacement from each other, and will form segments of a circular arc when added as vectors. The resulting relative intensity will depend upon the total phase displacement δ according to the relationship:
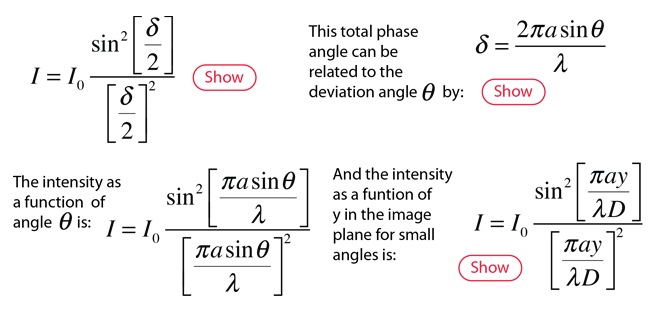
Diffraction concepts
Fraunhofer diffraction
Fraunhofer intensity concepts
Reference
Meyer-Arendt
Ed 4, Ch 14.
| HyperPhysics***** Light and Vision | R Nave |