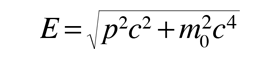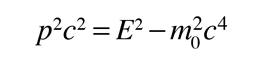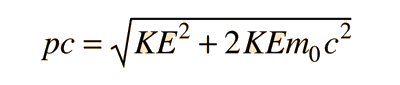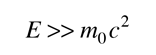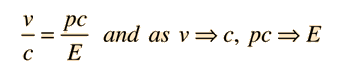DeBroglie Wavelength
A convenient form for the DeBroglie wavelength expression is
 |
where hc = 1239.84 eV nm and pc is expressed in electron volts. |
This is particularly appropriate for comparison with photon wavelengths since for the photon, pc=E and a 1 eV photon is seen immediately to have a wavelength of 1240 nm. For massive particles with kinetic energy KE which is much less than their rest mass energies:
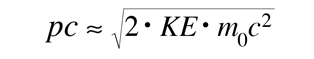 | ... | Show |
For an electron with KE = 1 eV and rest mass energy 0.511 MeV, the associated DeBroglie wavelength is 1.23 nm, about a thousand times smaller than a 1 eV photon. (This is why the limiting resolution of an electron microscope is much higher than that of an optical microscope.)
The following calculation uses the full relativistic expressions for kinetic energy, etc.
Caution! Since this calculation was designed for speeds which are a significant fraction of the speed of light, it may lose some accuracy for very low speeds. Under those conditions, small differences between large numbers occur in the calculations. For low speed calculations like the baseball example, it might be more accurate to use the non-relativistic calculation.
Low velocity calculation of DeBroglie wavelength |
| HyperPhysics***** Quantum Physics | R Nave |